토목기사 요약/수리수문학/개수로
출제 기준
[편집]2019-2021
- 전수두 및 에너지 방정식
- 효율적 흐름 단면
- 비에너지
- 도수
- 점변 부등류
- 오리피스
- 위어
용어 설명
[편집]수심, 수위
[편집]- 수심(水深, depth of flow) : 공기와 물이 접하는 자유수면에서 수로 바닥까지의 연직 거리.[1][2]
- 수위(水位, stage) : 자유수면으로부터 임의의 지점까지의 연직 거리.[3][4]
수리평균심
[편집]hydraulic mean depth. = 수리심, 수리수심(hydraulic depth)[3][5][6]
91
수로의 평균 수심
- 수로 폭 B (top width): 자유 수면에서의 수로 단면 폭
단면계수
- 등류 계산 시
- 한계류 계산 시
통수능
[편집]통수능 : 단면이 물을 통수시킬 수 있는 능력. 에서
Manning 공식에서 통수능
- n : Manning 조도계수
효율적 흐름 단면
[편집]♣♣♣13-2, 16-2, 19-2
일정 단면적에서 최대 유량이 흐르는 단면. 즉 경심 R(수리평균심, 동수반경, 수리반경)이 최대이거나 윤변 P가 최소인 단면. 직사각형 단면이던 사다리꼴 단면이던 반원이 내접되어야 한다.
- 직사각형 단면 B = 2h, ♣♣♣
- 정다각형을 반으로 자른 단면이 수리학적으로 유리한 단면이다!!!
비에너지
[편집]18-1, 18-2, 18-3, 19-1
- ♣♣♣ 비에너지는 수로 바닥을 기준으로 한 단위무게의 물 에너지. 등류에선 일정.
15-1, 16-4, 19-2
따라서 비에너지는 유량이 일정한 경우 수심만의 함수가 된다.
한계수심 : 비에너지가 최소일 때의 수심. 혹은 유량이 최대일 때의 수심 (정의 ♣♣14-2, 19-1, 19-3)
-
♣♣♣14-1, 15-1, 16-4, 19-3
95

개수로 단면이 오른쪽 그림처럼 w1에서 w2로 감소했다. 이때 수심 변화는 어떻게 될까?
풀이
- 상류인 경우: w2에서 유속 빨라짐. 수심 감소
- 사류인 경우: w2에서 유속 느려짐. 수심 증가
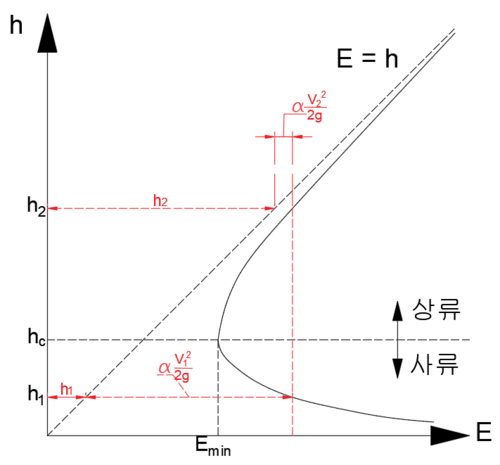
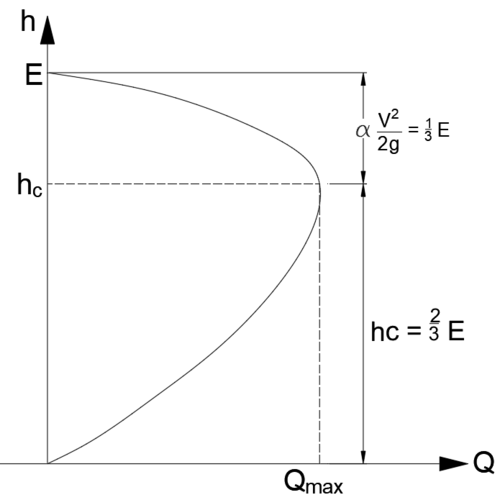
이유는 다음 그래프로 생각해보면 됨. 단위폭당 유량에 따른 수심변화와, 속도 수두가 어떻게 될 것인지....

수중 구조물이 있는 경우 수면 변화
[편집]상류의 흐름에 수중보를 설치하는 경우. 편의상 비에너지의 손실은 없다고 가정.

이것은 수로 바닥면이 z만큼 높아진 상태에서의 비에너지이다. 원래의 수로 바닥면과는 z의 높이만큼 비에너지 차이가 날 것이다. 비에너지의 손실은 없다고 하였으므로 1단면과 2단면의 비에너지가 같아야 한다. 이것을 식으로 나타낸다면

상류 흐름에 수중보를 설치하면 보가 있는 부분에서 수위는 감소. 같은 방법으로 사류일 때를 확인해보면 반대로 수위가 증가.
사각형 단면 한계수심
[편집]12-3, 18-3, 19-3
97, 18-3
직사각형 수로에서 폭이 5m, 한계수심이 1m, 에너지 보정계수 α = 1.0이면 유량은?
흐름의 상태
[편집]단면 변화 정도에 따른 분류
[편집]- 점변류(gradually varied flow) : 수면 변화가 완만하게 나타나는 흐름
- 급변류(rapidly varied flow) : 비교적 짧은 구간에서 급격한 수면 변화를 나타내는 흐름

레이놀즈 수에 의한 흐름의 분류
[편집]토목기사 요약/수리수문학/동수역학#층류, 난류의 구분 참고.
상류, 사류, 한계류
[편집]지배단면(control section)이란? (14-1)
- 개수로 흐름이 상류에서 사류로 바뀔 때 한계수심이 발생하는 단면[7]
- 한계경사 : 지배단면에서의 경사
♣♣ 계산문제, 개념 묻는 문제(13-1, 16-4, 19-1) 출제
장파전달속도 에 대하여
- 상류(subcritical flow, ordinary flow, tranquil flow): 한계수심보다 수심이 깊지만 한계유속보다 유속이 느린 흐름.(18-3) V < c. 장파가 상류로 전달.
- I < Ic
- 한계류(critical flow) : Fr = 1. 이때의 수심을 한계수심, 유속을 한계유속
- 사류(supercritical flow, jet flow, rapid flow): V > c. 하류 흐름의 영향이 상류로 전파되지 않음.
- I > Ic
Froude 수는 중력에 대한 관성력의 비
비력
[편집]비력(specific force, 충력치, 14-2, 15-3, 18-1) : 개수로 어떤 단면에서 단위중량 당 정수압 + 운동량
운동량 방정식으로부터 유도된다.

비력 = 정수압 + 운동량이므로
M1 = M2
참고 서적
- 김경호 (2010). 〈11. 개수로 정상흐름의 기초〉. 《수리학》. 한티미디어.
도수
[편집]= hydraulic jump. 흐름이 사류에서 상류로 변할 때 수면이 불연속적으로 뛰는 현상. 가지고 있는 에너지의 일부를 와류와 난류를 통해 소모한다.(15-1)
도수 전후 두 수심 : 공액수심[8]
도수 후 수심 = 도수고
♣♣♣12-3, 14-3, 15-2, 16-1, 19-3
직사각형 단면에 대해
도수 전후 비력이 일정함을 이용해 유도됨.(단위폭당 유량, 이차방정식 근의 공식, 프루드 수 등을 이용해 유도)
도수로 인한 에너지 손실
♣♣♣13-1, 14-2, 19-2, 19-3
비에너지 차이, 도수 전후 수심 유도 과정 중 나오는 식을 이용해 유도함.
참고 서적
- 김경호 (2010). 〈11. 개수로 정상흐름의 기초〉. 《수리학》. 한티미디어.
점변 부등류
[편집]부등류의 수면곡선
[편집]구분하는 것 문제로 나옴.
한계수심, 한계경사는 유량, 단면이 정해지면 하나로 정해짐
- 배수곡선(backwater curve) : . 상류(subcritical flow) 흐름에 댐, 위어 등을 설치하면 흐름을 따라 상류(上) 수심이 증가하는 곡선.(13-2, 18-1, 19-1)
- 저하곡선 : . 흐름을 따라 수심이 감소하는 곡선.
- 이면 수심은 일정하게 되어 등류가 됨. 여기서 h0는 등류수심.(임의 경사의 무한한 길이의 개수로에 물이 흐를 때 수심을 등류수심이라 함) 수로 경사를 완경사에서 점점 올려서 급경사로 만들수록 등류수심은 감소하다가 한계수심과 같아졌다가(한계경사) 한계수심보다 작아짐.(급경사)
수로경사를 S0, 한계경사를 Sc라 할 때,
- S0 < Sc이면 완경사(Mild slope; M)
- S0 = Sc이면 한계 경사(Critical slope; C)
- S0 > Sc이면 급경사(Steep slope; S)
- S0 = 0이면 바닥 경사는 수평(Horizontal; H)
- S0 < 0이면 역경사(Adverse; A)
여기에 따른 수면형은(15-1)

등류수심 h0에는 수면이 점근하고, 수로바닥과 한계수심 hc에는 급격하게 붙어버린다.
예시 - Mild slope
- 영역 1 : 이면 : M1곡선
- 영역 2 : 이면 : M2곡선
- 영역 3 : 이면 : M3곡선
참고 자료
- 김경호 (2010). 《수리학》. 한티미디어.
오리피스
[편집]- w:토리첼리의 정리는 위치수두를 속도 수두로 바꾸는 경우다.(95)
오리피스 유량
[편집]♣♣♣98, 00, 01, 02, 03, 12-3, 14-1, 14-2, 16-4, 19-3
유량계수
-
- 표준단관
- a : 수축단면(vena contracta)의 단면적
- A : 오리피스 단면적
- Cv : 유속계수
- 유량 (92, 19-1)
- 연직오리피스에서 유량계수 C는 대강 0.6 전후임(16-1)
작은 오리피스
[편집]
H > 5d이면 작은 오리피스
99, 14-3, 15-1, 20-1+2
이론 유속
- H : 수면에서 수축단면 중심까지 거리
실제 유속
95, 19-2, 20-1+2
오리피스 수두 오차와 유량 오차의 관계
오리피스 접근 유속 수두
큰 오리피스
[편집]- 상하단 압력차(수두변화)를 무시할 수 없을 때 큰 오리피스로 취급.(94, 96)
- 오리피스 단면 내 유속 분포가 동일치 않다고 보고 계산.(96)
H < 5d이면 큰 오리피스
- H : 오리피스 중심에서 수면까지 수두
- d : 오리피스 직경

베르누이 방정식과 연속방정식을 결합한 뒤, 적분하여 유도[9]
접근유속 고려 시
수중 오리피스
[편집]16-2
수문

- : 수문개방높이
얘도 똑같이 토리첼리 정리네
오리피스 유출 시간
[편집]
보통 오리피스(99)
연속방정식, 토리첼리 정리를 이용, 수면 강하 속도를 T에 대해 적분해서 얻은 식.[10]
- A : 수면적
- : 처음 수위
- : 나중 수위
수중 오리피스(13-3)
- : 1수조 수면적
- : 2수조 수면적
- : 처음 수위차
- : 나중 수위차

노즐
[편집]
12, 18-2
유량
노즐 전 점과 vena contracta 사이에서 베르누이 정리 이용. 연속방정식 이용하여 유도.
위어
[편집]98, 99
- 개수로 유량 측정, 취수를 위한 수위 증가 등의 목적으로 설치됨.
- 작은 유량 측정 시 삼각 위어가 효과적(16-2)
- 위어를 월류하는 흐름은 일반적으로 상류에서 사류로 변함.(16-2)
- 하류수위 이면 수중위어(14-1)
- H : 상류 전수두(기준면은 위어 상면)
위어 월류 유량 공식의 일반형(02, 13-3)
- C : 월류 계수
- L : 월류 폭
사각형 위어
[편집]유량
[편집]
15-2
베르누이 방정식과 연속방정식을 결합한 뒤, 적분하여 유도[11][12][13]
프란시스 유량 산정 공식
[편집]01, 02, 18-3
- n : 양단 수축 2, 일단수축 1, 수축 없으면 0
- h : 월류수심
단수축 폭
18-1
- 직사각형 수로에서 월류 수두 h와 유량 Q의 관계(99, 00, 12, 16-3, 19-1, 19-2)
광정 위어
[편집]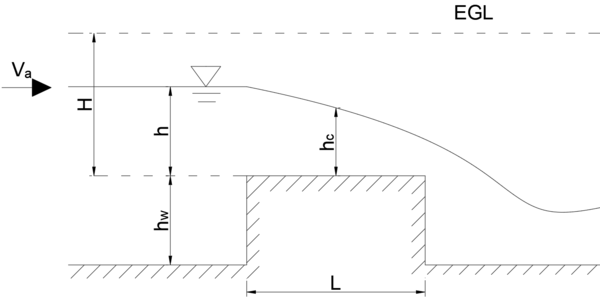
broad crest weir. 월류수심 h에 비해 위어 마루 폭 L이 큰 경우.(L > 0.7h)
(05, 13-1, 14-2, 20-1+2 ♣♣)
위어 상류의 한 지점과, 위어에서 한계수심 나타나는 한 지점사이에 베르누이 정리 사용하여 유량 공식 유도.
그림을 정확히 이해하고 유량 공식을 암기하기
- H : 전수두(h + ha)
- h : 월류수심
- : 접근유속
사다리꼴 광정 위어
[편집]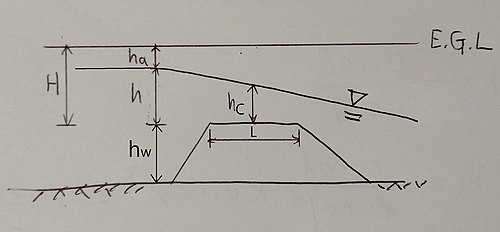
홈마 공식(실험에 의한 것)
2. 96
(사다리꼴) 광정위어에서 유량이 30m3/s일 때 위어 상면 수심은? 위어 폭이 5m, C = 0.4
삼각형 위어
[편집]
♣♣♣97, 00, 01, 13-2, 14-3, 15-1
- C : 유량계수
삼각형 수로에서 월류 수두 h와 유량 Q의 관계(93, 97, 98)
각주
[편집]- ↑ 송재우. 《수리학》 3판. 구미서관. 187쪽.
- ↑ 김경호 (2010). 《수리학》. 한티미디어. 513쪽.
- ↑ 3.0 3.1 송재우. 《수리학》 3판. 구미서관. 188쪽.
- ↑ 김경호 (2010). 《수리학》. 한티미디어. 514쪽.
- ↑ 김경호 (2010). 《수리학》. 한티미디어. 515쪽.
- ↑ Clayton T. Crowe 외. 《유체역학》 9판. 한티미디어. 647쪽.
- ↑ 김경호 (2010). 《수리학》. 한티미디어. 534쪽.
- ↑ 김경호 (2010). 《수리학》. 한티미디어. 539쪽.
- ↑ 전일권 외 (2009). 《수리학》. 동화기술. 311쪽.
- ↑ 김경호. 《수리학》 초판. 한티미디어. 269쪽.
- ↑ 송재우. 《수리학》 3판. 구미서관. 293쪽.
- ↑ Clayton T. Crowe 외. 《유체역학》 9판. 한티미디어. 562쪽.
- ↑ 전일권 외 (2009). 《수리학》. 동화기술. 297쪽.
참고 문헌
[편집]- 전일권 외 (2009). 《수리학》. 동화기술.














































![{\displaystyle T={\frac {2A_{1}A_{2}}{Ca{\sqrt {2g}}(A_{1}+A_{2})}}({\sqrt {H_{1}}}-{\sqrt {H_{2}}})\quad [sec]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f20a8d941f3db3cb2a78bcdeb259c4229f2396bb)

















