♣♣♣
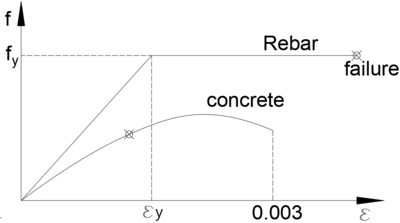
철근, 콘크리트 변형률은 중립축 거리에 비례.
콘크리트 압축연단 최대변형률(극한변형률) = 0.0033
철근은 완전 탄소성 거동.
ϵ
s
<
ϵ
y
{\displaystyle \epsilon _{s}<\epsilon _{y}}
f
s
=
E
s
ϵ
s
{\displaystyle f_{s}=E_{s}\epsilon _{s}}
ϵ
s
≥
ϵ
y
{\displaystyle \epsilon _{s}\geq \epsilon _{y}}
f
s
=
f
y
{\displaystyle f_{s}=f_{y}}
이거 조심!!! 압축철근 변형률
ϵ
s
′
{\displaystyle {\epsilon _{s}}'}
y 다!!!
콘크리트 인장강도는 무시
콘크리트 응력분포는 등가직사각형 응력분포. 이건 기사문제인데 원리는 똑같음. 유효깊이는 인장철근 도심까지 거리라서 압축철근이 있더라도 무시하고 인장철근만 가지고 계산하면 됨.
오른쪽 그림에서 유효깊이 d를 구하시오. D19 철근 공칭단면적은 287mm2
바리뇽의 정리를 이용하는 문제다.
5
d
=
2
×
350
m
m
+
3
×
450
m
m
{\displaystyle 5d=2\times 350mm+3\times 450mm}
d = 410mm
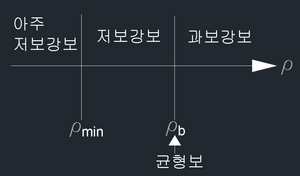
과보강 보. 콘크리트가 먼저 압축파괴. 철근은 항복도 못 했음.
저보강 보. 콘크리트가 극한변형률 (3)에 도달하기 전에 철근이 먼저 항복(2). 같은 번호 붙인 게 같은 순간의 응력, 변형률임.
아주 저보강 보. 압축부 콘크리트 변형률 이 0.003에 도달하기 전에 철근이 이미 인장파괴됨.
10, 11, 12, 13, 16
과다철근보, Over Reinforced Section
보의 연성 감소. 덜 처짐 .(철근비 증가 시. 자주 틀림. 철근 항복강도랑 처짐은 관계 없는듯?[ 1] [ 2]
과소철근보보다 휨강도는 약간 더 큼. 과소철근보[ 3]
인장 연성파괴 발생. 중립축이 압축부로 이동. Lightly Reinforced Section
인장 취성파괴 발생.(철근이 과다하게 늘어나면서 갑작스러운 파괴) 최소철근비 이상에서 인장철근비를 작게, 단면을 크게 하는 건 처짐제한에 유리한가?
(O) 단면 크면 단면이차모멘트가 커지니까 처짐값이 줄어든다. 최소철근비 이상에서 인장철근비를 줄이면 압축철근비가 늘어나야 한다. 때문에 처짐제한에 유리해진다.[ 4] ♣♣♣ 10, 11, 12, 15
균형철근비
ρ
b
=
0.85
β
1
f
c
k
f
y
0.003
0.003
+
ϵ
y
=
0.85
β
1
f
c
k
f
y
600
600
+
f
y
{\displaystyle {\begin{aligned}\rho _{b}&=0.85\beta _{1}{\frac {f_{ck}}{f_{y}}}{\frac {0.003}{0.003+\epsilon _{y}}}\\&=0.85\beta _{1}{\frac {f_{ck}}{f_{y}}}{\frac {600}{600+f_{y}}}\\\end{aligned}}}
최소철근비
ρ
m
i
n
=
[
0.25
f
c
k
f
y
,
1.4
f
y
]
m
a
x
{\displaystyle \rho _{min}=\left[{\frac {0.25{\sqrt {f_{ck}}}}{f_{y}}},{\frac {1.4}{f_{y}}}\right]_{max}}
최소철근비 계산에 두 식을 써서 비교하는 이유 : 콘크리트 강도가 커지면 취성이 증가하므로 이것도 반영한 것.
판정
ρ = ρb : 균형보
ρ > ρb : 과보강보
ρmin ≤ ρ < ρb : 저보강보
ρ
<
ρ
m
i
n
{\displaystyle \rho <\rho _{min}}
휨부재의 모든 단면에서 해석에 의해 필요한 철근량보다 1/3 이상 인장철근이 더 배치되는 경우 최소철근량 규정을 적용하지 않을 수 있다.(09, 12, 15)
정정구조물로써 플랜지가 인장 상태인 T형보 (예 : 캔틸레버로 된 T형보) 단면의 경우 최소철근량을 구하기 위한 식에서 bw 값은 플랜지 유효폭 b와 2bw 중 작은 값 사용.(15) 이거 계속 틀리네... 계산문제 있다. 최소철근비는 둘 중 큰값, 폭은 반대로 작은값! 2b와 bw 중 큰값일 리는 없지... 맨날 2b가 클테니까 예제
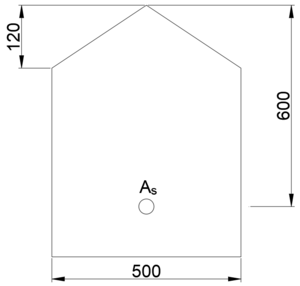
우측 그림에서 최소철근량 계산하기
b
0
=
[
b
,
2
b
w
]
m
i
n
{\displaystyle b_{0}=[b,2b_{w}]_{min}}
A
s
,
m
i
n
=
[
1.4
f
y
b
0
d
,
0.25
f
c
k
f
y
b
0
d
]
m
a
x
{\displaystyle A_{s,min}=\left[{\frac {1.4}{f_{y}}}b_{0}d,\ {\frac {0.25{\sqrt {f_{ck}}}}{f_{y}}}b_{0}d\right]_{max}}
b나 bw 넣는 게 아님!!!!
하지만 플랜지가 압축되는 통상의 T형보는 최소철근량 계산 시 bw 사용! 판정이 단철근 직사각형보로 되든, T형보로 되든 bw 를 넣어 검토한다![ 5]
두께가 균일한 구조용 슬래브, 기초판에 대해 경간방향으로 보강되는 인장철근 최소 단면적은 수축, 온도철근량에서 규정한 값과 같아야 한다. 이때 철근 최대 간격은 슬래브 또는 기초판 두께의 3배와 450mm 중 작은 값을 초과하지 않아야 한다.
fy (MPa)
최소 허용 인장변형률 εtmin
400 이하
0.004
400 초과
2.0
ϵ
y
{\displaystyle 2.0\epsilon _{y}}
ρ
m
a
x
=
0.85
β
1
f
c
k
f
y
0.003
0.003
+
ϵ
t
m
i
n
{\displaystyle \rho _{max}=0.85\beta _{1}{\frac {f_{ck}}{f_{y}}}{\frac {0.003}{0.003+\epsilon _{tmin}}}}
이건 최소 허용인장변형률 에 대한 값이고 인장지배한계 에 대한 최대철근비도 있는데 그냥
ϵ
t
m
i
n
{\displaystyle \epsilon _{tmin}}
y 넣으면 됨.
최대철근비 식을 균형철근비 공식과 조합하면
ρ
m
a
x
=
ϵ
c
+
ϵ
y
ϵ
c
+
ϵ
t
m
i
n
ρ
b
=
0.003
+
ϵ
y
0.003
+
ϵ
t
m
i
n
ρ
b
{\displaystyle {\begin{aligned}\rho _{max}&={\frac {\epsilon _{c}+\epsilon _{y}}{\epsilon _{c}+\epsilon _{tmin}}}\rho _{b}\\&={\frac {0.003+\epsilon _{y}}{0.003+\epsilon _{tmin}}}\rho _{b}\\\end{aligned}}}
♣♣♣
b = 300mm, d = 400mm, As = 250mm2 , fck = 24MPa, fy = 400MPa인 단철근 직사각형 보의 파괴형태는?
철근비를 구한 뒤, 균형철근비, 최소철근비를 가지고 파괴 유형을 결정한다.
ρ
=
A
s
b
d
=
0.0021
{\displaystyle \rho ={\frac {A_{s}}{bd}}=0.0021}
β
=
0.85
{\displaystyle \beta =0.85}
ρ
b
=
0.85
f
c
k
β
f
y
⋅
600
600
+
f
y
=
0.0260
{\displaystyle {\begin{aligned}\rho _{b}&={\frac {0.85f_{ck}\beta }{f_{y}}}\cdot {\frac {600}{600+f_{y}}}\\&=0.0260\\\end{aligned}}}
ρ
<
ρ
b
{\displaystyle \rho <\rho _{b}}
최소철근비는 변형률도에서 최외단 인장철근 변형률 구해서 하는 게 아님!! 설계기준에서 정하는 공식 으로 구하는 거다!! 깜빡하지 말자. 최외단 인장철근 변형률 활용하는 건 지배단면 구할 때임
1.4
f
y
=
0.0035
{\displaystyle {\frac {1.4}{f_{y}}}=0.0035}
0.25
f
c
k
f
y
=
0.00306
{\displaystyle {\frac {0.25{\sqrt {f_{ck}}}}{f_{y}}}=0.00306}
ρ
<
ρ
m
i
n
=
0.0035
{\displaystyle \rho <\rho _{min}=0.0035}
따라서 아주 저보강된 단면이며, 찢어짐 파괴가 일어난다.
원리 이해하기. 균형보 뿐만 아니라 다른 것도 중립축 위치 자주 물어봄. 00, 05, 12, 15, 16
05, 12
c
b
=
0.003
0.003
+
ϵ
y
d
=
600
600
+
f
y
d
{\displaystyle c_{b}={\frac {0.003}{0.003+\epsilon _{y}}}d={\frac {600}{600+f_{y}}}d}
그림과 같은 단면 보가 균형상태에 있다. 압축부 콘크리트에 작용하는 압축력은?
f
c
k
=
20
M
P
a
,
f
y
=
300
M
P
a
{\displaystyle f_{ck}=20MPa,\ f_{y}=300MPa}
중립축 cb 를 구하고 등가직사각형 응력블록 깊이 a를 계산해야된다. 착각하면 안 되는 게, 등가직사각형 응력블록 깊이를 c로 하면 안 된다!
c
b
0.003
=
600
0.0045
{\displaystyle {\frac {c_{b}}{0.003}}={\frac {600}{0.0045}}}
cb = 400mm
A
=
1
2
×
500
×
120
+
500
×
220
=
140000
m
m
2
{\displaystyle {\begin{aligned}A&={\frac {1}{2}}\times 500\times 120+500\times 220\\&=140000mm^{2}\\\end{aligned}}}
C
=
0.85
f
c
k
A
=
2380
k
N
{\displaystyle C=0.85f_{ck}A=2380kN}
오른쪽 그림과 같은 단면 보에 중립축 거리 c에 작용하는 압축응력을 등가직사각형 응력분포로 환산하여 빗금친 부분으로 나타내었다. As = 2040mm2 , fck = 24MPa, fy = 400MPa일 때 c는?
0.85
f
c
k
A
=
A
s
f
y
{\displaystyle 0.85f_{ck}A=A_{s}f_{y}}
0.85
×
24
(
100
2
×
2
+
400
x
)
=
2040
×
400
{\displaystyle 0.85\times 24(100^{2}\times 2+400x)=2040\times 400}
x = 50mm
a가 빗금 부분의 하단까지 거리 임!!!!!! 이게 핵심이다. 즉 a = 100 + 50 = 150mm인 것!!
β
c
=
0.85
c
=
150
m
m
{\displaystyle \beta c=0.85c=150mm}
c
=
150
0.85
=
176
m
m
{\displaystyle c={\frac {150}{0.85}}=176mm}
인장지배단면이라고 알려주더라도 이건 Φ 알려준 거고, 강도 계산에 쓰이는 c 구할 땐 다음 식으로 계산.
0.85
f
c
k
β
c
b
=
A
s
f
y
{\displaystyle 0.85f_{ck}\beta cb=A_{s}f_{y}}
변형률도 가지고 c 구하는 게 아님.
인장철근량, 항복강도를 늘려주면 어느 정도까지는 설계강도 역시 증가하다가 다시 감소함.
09
압축측 연단 콘크리트 변형률이 극한변형률 εcu = 0.003에 도달했을 때 최외단 인장철근 순인장변형률 εt 크기에 따라 부재 단면을 압축지배단면(Compression Controlled Section), 인장지배단면(Tension Controlled Section), 변화구간단면(Transition Region)으로 구분한다.
순인장변형률이란 프리스트레스 힘, 크리프, 건조수축, 온도변화에 의한 변형률을 고려하지 않은 인장변형률!
변화구간 13, 14, 15, 16 ♣♣♣
11, 14, 15 ♣♣♣ 자꾸 깜빡하고 엉뚱한 값 넣지 않도록 조심!!!!!!!! 자꾸 실수한다. 특히 최대철근비(량) 구할 때!
철근 종류
압축지배 변형률 한계
최소허용변형률 εmin
인장지배 변형률 한계
SD 400 이하
εy
0.004
0.005
SD 400 초과
εy
2.0εy
2.5εy
PS 강재
0.002
-
0.005
프리스트레스를 받지 않는 휨부재 또는 휨모멘트와 축력을 받지 않는 부재로 계수축력이
0.10
f
c
k
A
g
{\displaystyle 0.10f_{ck}A_{g}}
작은 경우 공칭축강도 상태에 있어 순인장변형률 εt 가 휨부재 최소허용변형률 이상이어야 한다. 주의
철근의 항복강도가 바뀔 때(예 : SD 500 으로 주면 깜빡하고 낚임) 압축, 인장지배 변형률 한계 바뀌는 것 까먹지 말기!! ♣♣♣
변화구간단면이라고 단정짓기 전에... 습관적으로 최소허용변형률보다 εt 가 큰지 확인!!! 아니라면 단면 확대 또는 철근을 줄여줘야 함!(연성 증가 필요) 표피철근(skin reinforcement). 보 또는 장선의 깊이 h가 900mm를 초과하면 종방향 표피 철근을 인장 연단으로부터 h/2 지점까지 부재 양 측면을 따라 균일하게 배치해야 한다.
과다철근보가 될 때에는 압축철근을 배치하는 게 좋다.(O) 콘크리트가 먼저 압축파괴되려 하니까 압축철근으로 압축력을 같이 받아주면 좋겠지? 압축철근 효과
지속하중에 의한 장기 처짐 감소(크리프 억제)
연성 증대
인장지배단면 파괴 유도
철근 조립 쉽게 함.(전단 철근)
단철근 보에 비해 압축철근이 들어간다고 휨 내력이 크게 증가하진 않는다 .
정(+), 부(-) 모멘트가 반복 작용하는 경우 구조체 안전성을 높임.
0.85
f
c
k
a
b
+
A
s
′
f
y
=
A
s
f
y
{\displaystyle 0.85f_{ck}ab+{A_{s}}'f_{y}=A_{s}f_{y}}
0.85
f
c
k
a
b
=
f
y
(
A
s
−
A
s
′
)
{\displaystyle 0.85f_{ck}ab=f_{y}(A_{s}-{A_{s}}')}
a
=
(
A
s
−
A
s
′
)
f
y
0.85
f
c
k
⋅
b
{\displaystyle a={\frac {(A_{s}-{A_{s}}')f_{y}}{0.85f_{ck}\cdot b}}}
압축철근 항복 변형률
ϵ
s
′
=
c
−
d
′
c
×
0.003
≥
ϵ
y
{\displaystyle {\epsilon _{s}}'={\frac {c-d'}{c}}\times 0.003\geq \epsilon _{y}}
0.85
f
c
k
a
b
+
A
s
′
f
y
=
A
s
f
y
{\displaystyle 0.85f_{ck}ab+{A_{s}}'f_{y}=A_{s}f_{y}}
y 로 놓지 말고 εs 로 놓기 !! 착각하지 말자. 인장철근이 항복한다고 하더라도
ϵ
s
≥
ϵ
y
{\displaystyle \epsilon _{s}\geq \epsilon _{y}}
ϵ
s
=
ϵ
y
{\displaystyle \epsilon _{s}=\epsilon _{y}}
f
s
=
f
y
{\displaystyle f_{s}=f_{y}}
공칭강도 : 복철근보는 단철근 직사각형보가 부담할 수 있는 휨모멘트와, 압축철근과 이에 해당하는 인장철근이 부담할 수 있는 휨모멘트로 구분하여 계산.
M
n
=
M
n
1
+
M
n
2
=
(
A
s
−
A
s
′
)
f
y
(
d
−
a
2
)
+
A
s
′
f
y
(
d
−
d
′
)
{\displaystyle {\begin{aligned}M_{n}&=M_{n1}+M_{n2}\\&=(A_{s}-{A_{s}}')f_{y}\left(d-{\frac {a}{2}}\right)+{A_{s}}'f_{y}(d-d')\\\end{aligned}}}
설계강도 계산 시 강도감소계수 Φ는 최외단 인장철근 변형률 εt 이용해서 계산해주어야 함. 그냥 0.85가 아님! 최소철근량은 검토하라고 단계에 나와있긴 한데 예제풀이엔 안 했다. 그냥 안전빵으로 하면 좋을 듯.
[ 편집 ]
A
s
f
y
=
0.85
f
c
k
a
b
+
A
s
′
f
y
{\displaystyle A_{s}f_{y}=0.85f_{ck}ab+{A_{s}}'f_{y}}
복철근 보 균형철근비
ρ
b
¯
=
A
s
b
d
{\displaystyle {\overline {\rho _{b}}}={\frac {A_{s}}{bd}}}
단철근 보 균형철근비
ρ
b
{\displaystyle \rho _{b}}
압축철근비
ρ
′
{\displaystyle \rho '}
이 담에 몇 가지 깜빡하는데, 균형철근비니까 b 들어가고, 좌변에 '바' 들어가는 거 까먹지 말자.
ρ
b
¯
b
d
f
y
=
0.85
f
c
k
β
c
b
+
ρ
′
b
d
f
y
{\displaystyle {\overline {\rho _{b}}}bdf_{y}=0.85f_{ck}\beta cb+\rho 'bdf_{y}}
ρ
b
¯
=
0.85
β
f
c
k
f
y
c
d
+
ρ
′
⋯
(
1
)
{\displaystyle {\overline {\rho _{b}}}=0.85\beta {\frac {f_{ck}}{f_{y}}}{\frac {c}{d}}+\rho '\qquad \cdots (1)}
∴
ρ
b
¯
=
ρ
b
+
ρ
′
{\displaystyle \therefore {\overline {\rho _{b}}}=\rho _{b}+\rho '}
[ 편집 ]
ρ
m
i
n
¯
=
0.85
β
f
c
k
f
y
d
′
d
0.003
0.003
−
ϵ
y
+
ρ
′
{\displaystyle {\overline {\rho _{min}}}=0.85\beta {\frac {f_{ck}}{f_{y}}}{\frac {d'}{d}}{\frac {0.003}{0.003-\epsilon _{\color {red}y}}}+\rho '}
분모에 마이너스다!
우측 첫번째 항은 변형률도에서 c에 대해 정리한 다음 위 (1)식에 넣어준 것임.
ϵ
s
′
c
−
d
′
=
0.003
c
{\displaystyle {\frac {{\epsilon _{s}}'}{c-d'}}={\frac {0.003}{c}}}
ϵ
y
c
−
d
′
=
0.003
c
{\displaystyle {\frac {\epsilon _{y}}{c-d'}}={\frac {0.003}{c}}}
c
=
0.003
0.003
−
ϵ
y
d
′
{\displaystyle c={\frac {0.003}{0.003-\epsilon _{y}}}d'}
[ 편집 ] 복철근보는 단철근보에 비해 과다철근보. 따라서 일반적으로
ρ
m
i
n
¯
≥
ρ
m
i
n
{\displaystyle {\overline {\rho _{min}}}\geq \rho _{min}}
복철근 보의 인장철근비 상한
ρ
m
a
x
¯
=
ρ
m
a
x
+
ρ
′
{\displaystyle {\overline {\rho _{max}}}=\rho _{max}+\rho '}
ρ
m
a
x
{\displaystyle \rho _{max}}
[ 편집 ] 등호 다 들어감. 오른쪽 세 개는 전부 '바' 들어감.
(
ρ
m
i
n
≤
)
ρ
m
i
n
¯
≤
ρ
¯
≤
ρ
m
a
x
¯
{\displaystyle (\rho _{min}\leq )\ {\overline {\rho _{min}}}\leq {\overline {\rho }}\leq {\overline {\rho _{max}}}}
A
s
f
y
=
0.85
f
c
k
a
b
+
A
s
′
f
s
′
=
(
A
s
−
A
s
′
)
f
y
+
A
s
′
f
s
′
{\displaystyle {\begin{aligned}A_{s}f_{y}&=0.85f_{ck}ab+{A_{s}}'{f_{s}}'\\&=(A_{s}-{A_{s}}')f_{y}+{A_{s}}'{f_{s}}'\\\end{aligned}}}
우측 1항을 단철근보로 보면
ρ
b
=
A
s
−
A
s
′
b
d
{\displaystyle \rho _{b}={\frac {A_{s}-{A_{s}}'}{bd}}}
ρ
b
¯
b
d
f
y
=
ρ
b
b
d
f
y
+
ρ
′
b
d
f
s
′
{\displaystyle {\overline {\rho _{b}}}bdf_{y}=\rho _{b}bdf_{y}+\rho 'bd{f_{s}}'}
∴
ρ
b
¯
=
ρ
b
+
ρ
′
f
s
′
f
y
{\displaystyle \therefore {\overline {\rho _{b}}}=\rho _{b}+\rho '{\frac {{f_{s}}'}{f_{y}}}}
(
f
s
′
=
E
s
ϵ
s
′
=
E
s
[
0.003
−
d
′
d
(
0.003
+
ϵ
y
)
]
≤
f
y
)
{\displaystyle \left({f_{s}}'=E_{s}{\epsilon _{s}}'=E_{s}\left[0.003-{\frac {d'}{d}}(0.003+\epsilon _{y})\right]\leq f_{y}\right)}
ρ
m
a
x
¯
=
ρ
m
a
x
+
ρ
′
f
s
′
f
y
{\displaystyle {\overline {\rho _{max}}}=\rho _{max}+\rho '{\color {red}{\frac {{f_{s}}'}{f_{y}}}}}
ρ
m
i
n
≤
ρ
¯
≤
ρ
m
a
x
¯
{\displaystyle \rho _{min}\leq {\overline {\rho }}\leq {\overline {\rho _{max}}}}
인장, 압축철근 항복
인장철근만 항복
ρ
b
¯
{\displaystyle {\overline {\rho _{b}}}}
ρ
b
¯
=
0.85
β
f
c
k
f
y
c
d
+
ρ
′
{\displaystyle {\overline {\rho _{b}}}=0.85\beta {\frac {f_{ck}}{f_{y}}}{\frac {c}{d}}+\rho '}
∴
ρ
b
¯
=
ρ
b
+
ρ
′
{\displaystyle \therefore {\overline {\rho _{b}}}=\rho _{b}+\rho '}
∴
ρ
b
¯
=
ρ
b
+
ρ
′
f
s
′
f
y
{\displaystyle \therefore {\overline {\rho _{b}}}=\rho _{b}+\rho '{\frac {{f_{s}}'}{f_{y}}}}
(
f
s
′
=
E
s
ϵ
s
′
=
E
s
[
0.003
−
d
′
d
(
0.003
+
ϵ
y
)
]
≤
f
y
)
{\displaystyle \left({f_{s}}'=E_{s}{\epsilon _{s}}'=E_{s}\left[0.003-{\frac {d'}{d}}(0.003+\epsilon _{y})\right]\leq f_{y}\right)}
ρ
m
i
n
¯
{\displaystyle {\overline {\rho _{min}}}}
ρ
m
i
n
¯
=
0.85
β
f
c
k
f
y
d
′
d
0.003
0.003
−
ϵ
y
+
ρ
′
{\displaystyle {\overline {\rho _{min}}}=0.85\beta {\frac {f_{ck}}{f_{y}}}{\frac {d'}{d}}{\frac {0.003}{0.003-\epsilon _{y}}}+\rho '}
X
ρ
m
a
x
¯
{\displaystyle {\overline {\rho _{max}}}}
ρ
m
a
x
¯
=
ρ
m
a
x
+
ρ
′
{\displaystyle {\overline {\rho _{max}}}=\rho _{max}+\rho '}
ρ
m
a
x
¯
=
ρ
m
a
x
+
ρ
′
f
s
′
f
y
{\displaystyle {\overline {\rho _{max}}}=\rho _{max}+\rho '{\frac {{f_{s}}'}{f_{y}}}}
조건
(
ρ
m
i
n
≤
)
ρ
m
i
n
¯
≤
ρ
¯
≤
ρ
m
a
x
¯
{\displaystyle (\rho _{min}\leq )\ {\overline {\rho _{min}}}\leq {\overline {\rho }}\leq {\overline {\rho _{max}}}}
ρ
m
i
n
≤
ρ
¯
≤
ρ
m
a
x
¯
{\displaystyle \rho _{min}\leq {\overline {\rho }}\leq {\overline {\rho _{max}}}}
직사각형 보에 비해 큰 압축대폭 사용. 단, 슬래브가 휨인장을 받는 경우는 장점 거의 없음.
유효폭 증가 → 주철근량 줄일 수 있음.
큰 강성(EI). 처짐 감소
사용하중 하에서 콘크리트 압축응력 감소시켜 크리프에 의한 장기처짐 감소
직사각형 보에 비해 자중 감소, 재료 절약, 지간 길게 가능. 세 값 중 작은 값
16
t
f
+
b
w
{\displaystyle 16t_{f}+b_{w}}
양쪽 슬래브 중심간 거리 : 길이가 다를 수 있으니 조심!
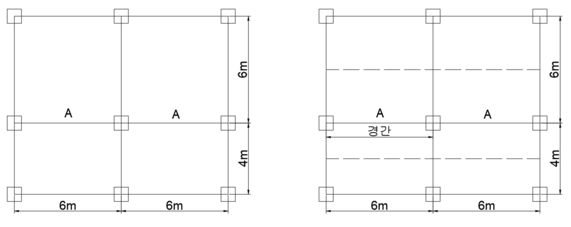
경간의 1/4 대칭 T형보 평면도를 보고 유효폭 구하는 문제. A로 표시한 부분이 T형보이다. 경간, 슬래브 중심간 거리를 잘 봐둘 것. T형보 플랜지, 복부 치수는 단면도를 통해 따로 주어지는데 그건 생략함. 슬래브 중심간 거리 구할 때, 치수가 보의 중심부터 나와있으니까 따로 복부폭 더해주면 안 된다!
세 값 중 작은 값
6
t
f
+
b
w
{\displaystyle 6t_{f}+b_{w}}
인접보와 내측거리
×
1
2
+
b
w
{\displaystyle \times {\frac {1}{2}}+b_{w}}
보 경 간
×
1
12
+
b
w
{\displaystyle {\text{보 경 간 }}\times {\frac {1}{12}}+b_{w}}
구한 유효폭 be 가 아래 계산에서 b로 쓰임.
t
f
≥
1
2
b
w
{\displaystyle t_{f}\geq {\frac {1}{2}}b_{w}}
b
e
≤
4
b
w
{\displaystyle b_{e}\leq 4b_{w}}
맨날 틀림. 맞춘 적이 없음 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ
T형보 플랜지가 인장 되는 경우 휨인장철근 을 유효플랜지 폭이나 경간 1/10 폭 중에서 작은쪽에 걸쳐 분포시킨다. 유효플랜지 폭이 경간의 1/10을 넘는 경우 추가로 축방향 철근을 배치해야 한다.(수축, 온도철근)
횡방향철근은 T형보 내민 플랜지를 캔틸레버로 보고 플랜지에 작용하는 계수하중 에 대해 설계(이때 독립 T형보는 내민플랜지 전폭을 유효폭으로 함). 횡방향철근 간격은 슬래브 두께 5배 이하, 450mm 이하
부(-)의 휨모멘트를 받고 있는 T형보의 중립축이 웨브 내에 있으면 웨브를 폭 으로 하는 직사각형보로 설계
정(+)의 휨모멘트를 받는 T형보에서 중립축이 가급적 플랜지 내에 들도록 설계하는 것이 유리
정(+)의 휨모멘트를 받는 T형보의 인장철근량
A
s
≤
0.85
f
c
k
b
t
f
f
y
{\displaystyle A_{s}\leq {\frac {0.85f_{ck}bt_{f}}{f_{y}}}}
일반적으로 T형보에서 웨브는 전단력 에, 플랜지는 휨 에 저항.
a
=
A
s
f
y
0.85
f
c
k
b
{\displaystyle a={\frac {A_{s}f_{y}}{0.85f_{ck}b}}}
a > tf : T형보
a ≤ tf : 폭이 b인 단철근 직사각형보 또는 플랜지 전체가 받는 압축력과 인장철근이 받는 인장력을 비교해서 판정해도 된다.
♣♣♣ 14-3, 15-1, 15-2, 18-1, 18-2 기사문제
fck = 21MPa, fy = 300MPa, b = 1000mm, tf = 60mm, bw = 300mm, d = 600mm, As = 4000mm2 일 때 설계휨강도 φMn 을 구하시오.
1) T형보 판정
전체에 대해서 응력블록의 깊이 a 계산 .
0.85
f
c
k
a
b
=
A
s
f
y
{\displaystyle 0.85f_{ck}ab=A_{s}f_{y}}
a = 67.2mm
a > tf 이므로 T형보로 해석한다.
2) 응력사각형 깊이 a 계산
플랜지 내민 부분 압축력에 대응하는 가상의 인장철근 단면적
Cf = Tf 에서
0.85
f
c
k
⋅
t
f
(
b
−
b
w
)
=
A
s
f
f
y
{\displaystyle 0.85f_{ck}\cdot t_{f}(b-b_{w})=A_{sf}f_{y}}
A
s
f
=
0.85
f
c
k
t
f
(
b
−
b
w
)
f
y
=
0.85
×
21
×
60
×
(
1000
−
300
)
300
=
2499
m
m
2
{\displaystyle {\begin{aligned}A_{sf}&={\frac {0.85f_{ck}t_{f}(b-b_{w})}{f_{y}}}\\&={\frac {0.85\times 21\times 60\times (1000-300)}{300}}\\&=2499mm^{2}\end{aligned}}}
Cw = Tw 에서
a
=
f
y
(
A
s
−
A
s
f
)
0.85
f
c
k
b
w
=
300
×
(
4000
−
2499
)
0.85
×
21
×
300
=
84.1
m
m
{\displaystyle {\begin{aligned}a&={\frac {f_{y}(A_{s}-A_{sf})}{0.85f_{ck}b_{w}}}\\&={\frac {300\times (4000-2499)}{0.85\times 21\times 300}}\\&=84.1mm\end{aligned}}}
Φ 계산(그냥 0.85가 아님 !!!!!!!!!!!!!)
β
=
0.85
{\displaystyle \beta =0.85}
c
=
a
β
=
84.1
0.85
=
98.94
m
m
{\displaystyle c={\frac {a}{\beta }}={\frac {84.1}{0.85}}=98.94mm}
ϵ
t
600
−
98.94
=
0.003
98.94
{\displaystyle {\frac {\epsilon _{t}}{600-98.94}}={\frac {0.003}{98.94}}}
ϵ
t
=
0.0152
>
ϵ
t
,
t
c
l
=
0.005
{\displaystyle \epsilon _{t}=0.0152>\epsilon _{t,\ tcl}=0.005}
∴
ϕ
=
0.85
{\displaystyle \therefore \phi =0.85}
3) 설계강도 Md
M
d
=
ϕ
M
n
=
ϕ
(
M
n
f
+
M
n
w
)
=
0.85
{
A
s
f
f
y
(
d
−
t
f
2
)
+
(
A
s
−
A
s
f
)
f
y
(
d
−
a
2
)
}
=
0.85
{
2499
×
300
(
600
−
60
2
)
+
(
4000
−
2499
)
×
300
×
(
600
−
84.1
2
)
}
=
576787802.3
N
⋅
m
m
=
576.79
k
N
⋅
m
{\displaystyle {\begin{aligned}M_{d}=\phi M_{n}&=\phi (M_{nf}+M_{nw})\\&=0.85\left\{A_{sf}f_{y}\left(d-{\frac {t_{f}}{2}}\right)+(A_{s}-A_{sf})f_{y}\left(d-{\frac {a}{2}}\right)\right\}\\&=0.85\left\{2499\times 300\left(600-{\frac {60}{2}}\right)+(4000-2499)\times 300\times \left(600-{\frac {84.1}{2}}\right)\right\}\\&=576787802.3N\cdot mm=576.79kN\cdot m\end{aligned}}}
최소철근량 검토도 잊지 말자.
보의 횡지지 간격은 압축플랜지 또는 압축면 최소폭의 50배 이하.
↑ 이학민 (2016). 《토목설계》. 탑스팟. 3 -97쪽. ↑ https://www.youtube.com/watch?v=5cF2lEZge0M ↑ 이학민 (2016). 《토목설계》. 탑스팟. 3 -58쪽. ↑ https://cafe.naver.com/tomokgisa/15706 ↑ 윤영수. 《철근콘크리트 역학 및 설계》 3판. 씨아이알. 173, 175쪽.

























![{\displaystyle \rho _{min}=\left[{\frac {0.25{\sqrt {f_{ck}}}}{f_{y}}},{\frac {1.4}{f_{y}}}\right]_{max}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b0013737fb580d63d11dfc34d5f15bde6a8475f)

![{\displaystyle b_{0}=[b,2b_{w}]_{min}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e38bb3cdfb57adebc6ec93509395e772a9dbb158)
![{\displaystyle A_{s,min}=\left[{\frac {1.4}{f_{y}}}b_{0}d,\ {\frac {0.25{\sqrt {f_{ck}}}}{f_{y}}}b_{0}d\right]_{max}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f26a60c1cfb5a966afeab0d07e9b7f6bbf221dbd)
















































![{\displaystyle \left({f_{s}}'=E_{s}{\epsilon _{s}}'=E_{s}\left[0.003-{\frac {d'}{d}}(0.003+\epsilon _{y})\right]\leq f_{y}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/398e700afb780b4a5737705442e8cdc0117bfbd2)
























