1. 80, 84, 87, 90, 14-2
모래 지반, 포화 단위중량 = 1.8t/m3 , 정지토압계수 0.5일 때 z = 5m 깊이 미소요소에 작용하는 수평방향 전응력은?
풀이
σ
h
=
K
0
σ
v
′
+
u
=
K
0
⋅
γ
s
u
b
⋅
z
+
γ
w
⋅
z
=
0.5
×
(
1.8
−
1
)
×
5
+
1
×
5
=
7
t
/
m
2
{\displaystyle {\begin{aligned}\sigma _{h}&=K_{0}{\sigma _{v}}'+u\\&=K_{0}\cdot \gamma _{sub}\cdot z+\gamma _{w}\cdot z\\&=0.5\times (1.8-1)\times 5+1\times 5\\&=7t/m^{2}\end{aligned}}}
♣♣♣
93, 97, 10 기출
모래의 포화밀도 2.0g/cm3 일 때 제일 아래 면의 유효응력은 얼마일까?
풀이
전응력 1×5 + 2×10 = 25g/cm2
공극수압 1×15 = 15g/cm2
유효응력 = 25 - 15 = 10g/cm2
89 기출
습윤 밀도 1.65t/m3 , 수중밀도 0.8t/m3 일 때 제일 바닥면에 작용하는 유효응력은?
풀이
σ
¯
=
γ
t
⋅
h
1
+
γ
s
u
b
⋅
h
2
=
1.65
×
3
+
0.8
×
2
=
6.55
t
/
m
2
{\displaystyle {\bar {\sigma }}=\gamma _{t}\cdot h_{1}+\gamma _{sub}\cdot h_{2}=1.65\times 3+0.8\times 2=6.55t/m^{2}}
예제 상재하중이 작용할 때의 유효응력
σ
=
Z
⋅
γ
s
a
t
+
q
{\displaystyle \sigma =Z\cdot \gamma _{sat}+q}
u
=
Z
⋅
γ
w
{\displaystyle u=Z\cdot \gamma _{w}}
σ
¯
=
σ
−
u
=
Z
(
γ
s
a
t
−
γ
w
)
+
q
=
Z
⋅
γ
s
u
b
+
q
{\displaystyle {\bar {\sigma }}=\sigma -u=Z(\gamma _{sat}-\gamma _{w})+q=Z\cdot \gamma _{sub}+q}
♣♣♣ 수리학 19-3
수직 유리 튜브(모세관)의 하단 끝에 임의의 액체가 놓여졌을 때, 메니스커스 (meniscus)가 형성된다. 액체 기둥의 높이는 Jurin's Law에 의해 주어진다. 표면장력을 T라고 할 때, T는 관벽으로부터 θ만큼 기울어져서 작용하며, 액체 기둥 최상단의 둘레 부분에 작용한다고 할 수 있다. 액체 기둥이 정지해 있으므로, 액체 기둥 자체의 무게(좌변)와 표면장력에 의한 힘(우변)이 같다.
π
R
2
h
γ
w
=
2
π
R
T
cos
θ
{\displaystyle \pi R^{2}h\gamma _{w}=2\pi RT\cos \theta }
메니스커스의 높이 h에 대해 정리하면
h
=
2
T
cos
θ
R
γ
w
{\displaystyle h={\frac {2T\cos \theta }{R\gamma _{w}}}}
접촉각 θ=0, 수온 15도일 때
h
=
0.3
D
{\displaystyle h={\frac {0.3}{D}}}
♣95, 05, 08, 10
모관 상승이 있는 부분은 음의 간극수압이 생겨 유효응력이 증가함
모관현상으로 지표면까지 포화되면 지표면 유효응력은 γw h
모관현상이 있을 때 지하수위는 공극수압이 0
모관 상승고는 점토 > 실트 > 모래 > 자갈(입경이 클수록 모관상승고 낮음) Hazen은 사질토 에서 모세관 상승 높이 h에 대하여 다음과 같은 실험식 을 제시하였다.
16-2
h
=
C
e
D
10
{\displaystyle h={\frac {C}{eD_{10}}}}
D10 : 모래의 유효입경 (mm)
e : 공극비
C : 상수(10 ~ 50) 모관현상 없을 때
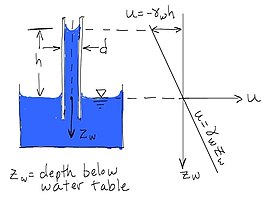
바닥면 유효응력 계산하기
σ
=
γ
1
(
h
1
+
h
2
)
+
γ
s
a
t
Z
{\displaystyle \sigma =\gamma _{1}(h_{1}+h_{2})+\gamma _{sat}Z}
u
=
γ
w
Z
{\displaystyle u=\gamma _{w}Z}
σ
¯
=
σ
−
u
=
γ
1
(
h
1
+
h
2
)
+
γ
s
u
b
Z
{\displaystyle {\begin{aligned}{\bar {\sigma }}&=\sigma -u\\&=\gamma _{1}(h_{1}+h_{2})+\gamma _{sub}Z\\\end{aligned}}}
모관현상 발생 시 : 모관현상 발생 시 부의 공극수압 발생. 유효응력은 증가.
기사 시험 출제되는데 암기보단 이해임.
모관현상에 의해 두번째 층까지 포화됨. 바닥면 유효응력은?
σ
=
Z
⋅
γ
s
a
t
+
h
2
⋅
γ
s
a
t
+
h
1
⋅
γ
1
=
γ
s
a
t
(
Z
+
h
2
)
+
γ
1
h
1
{\displaystyle {\begin{aligned}\sigma &=Z\cdot \gamma _{sat}+h_{2}\cdot \gamma _{sat}+h_{1}\cdot \gamma _{1}\\&=\gamma _{sat}(Z+h_{2})+\gamma _{1}h_{1}\\\end{aligned}}}
u
=
γ
w
Z
+
γ
w
h
2
−
γ
w
h
2
=
Z
γ
w
{\displaystyle u=\gamma _{w}Z+{\color {red}\gamma _{w}h_{2}}-\gamma _{w}h_{2}=Z\gamma _{w}}
σ
¯
=
σ
−
u
=
γ
s
a
t
(
Z
+
h
2
)
+
γ
1
h
1
−
Z
γ
w
=
Z
⋅
γ
s
u
b
+
γ
s
a
t
⋅
h
2
+
γ
1
h
1
{\displaystyle {\begin{aligned}{\bar {\sigma }}=\sigma -u&=\gamma _{sat}(Z+h_{2})+\gamma _{1}h_{1}-Z\gamma _{w}\\&=Z\cdot \gamma _{sub}+\gamma _{sat}\cdot h_{2}+\gamma _{1}h_{1}\\\end{aligned}}}
지하수위 이하의 흙은 부력을 받으니까
γ
s
u
b
=
γ
s
a
t
−
γ
w
{\displaystyle \gamma _{sub}=\gamma _{sat}-\gamma _{w}}
sub 가 아닌 γsat 을 그대로 쓴다.
88, 97, 99, 00 기출
지하수위는 지표 아래 1m에 있다. 모관현상으로 인해 지표면까지 물로 포화되어 있을 때 지하수위면에 작용하는 유효 연직응력 크기는? 흙의 포화단위중량은 1.8t/m3 이다.
풀이
σ
=
γ
s
a
t
⋅
1
m
=
1.8
t
/
m
2
{\displaystyle \sigma =\gamma _{sat}\cdot 1m=1.8t/m^{2}}
u
=
γ
w
⋅
1
m
−
γ
w
⋅
1
m
=
0
{\displaystyle u=\gamma _{w}\cdot 1m-\gamma _{w}\cdot 1m=0}
σ
¯
=
σ
−
u
=
1.8
t
/
m
2
{\displaystyle {\bar {\sigma }}=\sigma -u=1.8t/m^{2}}
96, 00, 08-1 기출
A점의 유효응력을 구하시오.
풀이
전응력 = 1.6×2 + 1.8×1 = 5t/m2
간극수압 = - γw · hc · S = - 1 · 2 · 0.40 = - 0.80 t/m2 (모관현상이 일어나면 부의 공극수압이 발생, 유효응력은 증대됨)
(hc : 지하수면부터 수압을 구하고자하는 점까지의 높이)
유효응력 = 전응력 - 간극수압 = 5.80 t/m2
포화도 있을 때만 일단 공극수압 식 따로 외워두자... 왜 완전포화일 때랑 차이가 나는 건지 모르겠다.
[ 편집 ] 연직응력 증가는 탄성계수 E와 관계 없음(95, 99, 19-3). 식 보면 알 수 있음. 89, 15-1, 19-2 / 실기 17-2
Δ
σ
z
=
−
3
P
2
π
R
2
cos
3
θ
=
3
P
2
π
Z
2
[
1
+
(
r
Z
)
2
]
5
2
=
I
σ
P
Z
2
{\displaystyle {\begin{aligned}\Delta \sigma _{z}&=-{\frac {3P}{2\pi R^{2}}}\cos ^{3}\theta \\&={\frac {3P}{2\pi Z^{2}\left[1+\left({\frac {r}{Z}}\right)^{2}\right]^{\frac {5}{2}}}}\\&=I_{\sigma }{\frac {P}{Z^{2}}}\\\end{aligned}}}
I
σ
=
영 향 계 수
=
3
2
π
1
{
1
+
(
r
Z
)
2
}
5
2
{\displaystyle I_{\sigma }={\text{영 향 계 수 }}={\frac {3}{2\pi }}{\frac {1}{\left\{1+\left({\frac {r}{Z}}\right)^{2}\right\}^{\frac {5}{2}}}}}
Δ
σ
r
=
P
2
π
[
3
r
2
Z
R
2
−
(
1
−
2
μ
)
(
R
⋅
Z
R
r
2
)
]
{\displaystyle \Delta \sigma _{r}={\frac {P}{2\pi }}\left[{\frac {3r^{2}Z}{R^{2}}}-(1-2\mu )\left({\frac {R\cdot Z}{Rr^{2}}}\right)\right]}
Δ
τ
z
r
=
3
P
2
π
⋅
r
Z
2
R
5
{\displaystyle \Delta \tau _{zr}={\frac {3P}{2\pi }}\cdot {\frac {rZ^{2}}{R^{5}}}}
S
=
q
B
1
−
μ
2
E
I
p
{\displaystyle S=qB{\frac {1-\mu ^{2}}{E}}I_{p}}
[ 편집 ] 18-3
Δ
σ
z
=
q
s
⋅
I
σ
{\displaystyle \Delta \sigma _{z}=q_{s}\cdot I_{\sigma }}
Iσ : 영향계수. = f(m, n) 구형 등분포 하중의 모서리에서만 영향계수 구할 수 있다. 구형 영역 밖의 응력증가량을 구하려면 사각형을 넓혀서 계산한 값에서 늘인 부분만큼에 의한 응력증가량을 빼준다.
m
=
B
Z
{\displaystyle m={\frac {B}{Z}}}
n
=
L
Z
{\displaystyle n={\frac {L}{Z}}}
Z : 응력증가량을 구하고자 하는 곳까지의 연직 깊이 B, L은 서로 바꿔서 넣어줘도 상관없다.
[ 편집 ] Newmark 영향원법(18-2)
95, 96, 97, 00, 01, 03, 13-1, 16-4 / 실기 17-1
Δ
σ
z
=
Q
(
B
+
z
)
(
L
+
z
)
=
P
B
L
(
B
+
z
)
(
L
+
z
)
{\displaystyle {\begin{aligned}\Delta \sigma _{z}&={\frac {Q}{(B+z)(L+z)}}\\&={\frac {PBL}{(B+z)(L+z)}}\\\end{aligned}}}
연속기초는 단위길이당 응력 증가량을 계산.
Δ
σ
z
=
P
B
⋅
1
B
+
Z
{\displaystyle \Delta \sigma _{z}={\frac {PB\cdot 1}{B+Z}}}
93, 18-1
Δ
σ
z
=
2
q
z
3
π
(
x
2
+
z
2
)
2
=
2
q
π
z
[
(
x
z
)
2
+
1
]
2
{\displaystyle \Delta \sigma _{z}={\frac {2qz^{3}}{\pi (x^{2}+z^{2})^{2}}}={\frac {2q}{\pi z\left[\left({\frac {x}{z}}\right)^{2}+1\right]^{2}}}}
♣♣♣
동상(frost heave) : 흙속의 온도가 영하로 내려가서 지표면 아래 흙속의 물이 얼어 지표면이 부풀어 오르는 현상.
연화(frost boil) : 동결 지반이 해빙되고 얼음 렌즈가 녹은 물이 빨리 배수되지 않으면 함수비가 원래보다 훨씬 커져 지반 강도가 저하되는 현상.(13-2)
12-3 / 실기 97-2
지하수위 : 동결 심도 하단에서 지하수면까지의 거리가 모관 상승고보다 작을 때
모관 상승고의 크기
흙의 투수도
동결 온도의 계속 기간
물이 얼면 9%정도 부피 증가.
동상현상은 지표면부터 아래쪽으로 진행됨. 95, 01, 07, 실기 06-2
점토는 동결이 장기간 계속될 때만 동상을 일으킨다.
동해 심한 순서: 실트 > 점토 > 모래 > 자갈. (실트질이 모관상승은 점토보다 작으나, 투수계수가 커서 물 공급이 많으므로 동상현상 큼.[ 1]
하층으로부터 물 공급이 충분하면 동상현상이 잘 일어난다.
깨끗한 모래는 모관 상승 높이가 작아 동상을 일으키지 않는다. 동상현상이 일어나면 함수비 증가(83, 97, 98) 실기 11-3, 19-3
Z
=
C
F
(
c
m
)
{\displaystyle Z=C{\sqrt {F}}\ (cm)}
F : 동결지수(°C·day) = 0도 이하 온도 절댓값 × 지속시간(일)
C : 지역에 따른 상수(3 - 5) 04, 06, 10 / ♣♣실기 09-3
배수구 설치, 지하수위 저하
모관수 상승 차단(조립의 차단층을 지하수위보다 높은 곳에 설치)
동결깊이보다 높게 있는 흙을 동결하지 않는 흙으로 치환
지표 흙을 화학약품 처리해 동결온도를 내림
지표 부근에 단열재료(석탄재, 코크스) 매립
↑ 한솔아카데미 실트 동상현상 질문
이인모 (2014). 《토질역학의 원리》. 씨아이알. 210-215쪽. 임진근 외, <<토목기사 과년도 - 토질 및 기초>>(2015), 성안당 출판사, 7장 지중 응력 



































![{\displaystyle {\begin{aligned}\Delta \sigma _{z}&=-{\frac {3P}{2\pi R^{2}}}\cos ^{3}\theta \\&={\frac {3P}{2\pi Z^{2}\left[1+\left({\frac {r}{Z}}\right)^{2}\right]^{\frac {5}{2}}}}\\&=I_{\sigma }{\frac {P}{Z^{2}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d6ce485680c2a55e6bcd7b94a6ba946a313f845)

![{\displaystyle \Delta \sigma _{r}={\frac {P}{2\pi }}\left[{\frac {3r^{2}Z}{R^{2}}}-(1-2\mu )\left({\frac {R\cdot Z}{Rr^{2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f5dcf15268311707c3cc6b10677123e1ead8073)







![{\displaystyle \Delta \sigma _{z}={\frac {2qz^{3}}{\pi (x^{2}+z^{2})^{2}}}={\frac {2q}{\pi z\left[\left({\frac {x}{z}}\right)^{2}+1\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/504e4ab357ecb6bebf09867d9a4aa9efc8d647db)
