토목기사 요약/응용역학/보의 처짐

기사 출제 1위 ♣♣♣

부호 약속

♣♣♣

처짐 : 하향 +, 상향 -
처짐각 : 변형 전 축 기준 시계방향 +, 반시계방향 -

곡률, 곡률반경

♣♣♣13-1

곡률

={\frac {1}{R}}={\frac {M}{EI}}

곡률반경

R={\frac {EI}{M}}

w(x) : 하중함수

$EI{\frac {d^{4}y}{dx^{4}}}=w(x)$

계산 방법

15-2 종류 물어봄

모멘트 면적법
탄성하중법 : 단순보에만
공액보법 : 내민보, 외팔보, 연속보에 적용 가능. 단순보에만 적용가능한 탄성하중법을, 이러한 형태의 보에도 가능하도록 보를 바꾼 것을 공액보라고 함.^[1] 뼈대에는 어려움
(공액구조법(conjugate structure method))
가상일법(가상단위하중법)
카스틸리아노의 제 2법칙^[2]

이 방법들은 부정정보, 골조와 트러스 반력 계산에도 사용된다.

그 외

이중적분법(Double Integration Method)

모멘트면적법

Saint Venant에 의해 발견. Mohr, Greene이 개선.^[3]

탄성곡선 : 보가 처졌을 때 형상 나타낸 곡선.

♣♣♣ 15-2, 16-1, 17-2 등등

제 1정리 : 부재 두 점에서 그은 탄성곡선 접선 사이 처짐각 변화량은 두 점 사이 ${\frac {M}{EI}}$ 도 면적과 동일

\theta _{AB}=\int _{A}^{B}{\frac {M}{EI}}dx

제 2정리 : 보의 탄성곡선 한 점에서의 접선이 탄성곡선의 다른 점과 이루는 상대적인 처짐량은 처짐을 계산코자 하는 점에서 취한 두 점 사이 ${\frac {M}{EI}}$ 도의 모멘트와 동일^[4]

\Delta _{AB}=\int _{A}^{B}{\frac {Mx}{EI}}dx

탄성하중법

♣♣♣

탄성하중 : 모멘트를 EI로 나눈 값. 이것을 하중으로 작용시키기 때문에 탄성 '하중'이라고 함.^[5]

17-4

A를 M/EI도의 면적이라고 하면, 처짐( $\Delta$ )은 $\Delta _{L}=Ax,\Delta _{R}=Ay$ 이고, 두 접선 사이의 각은 A이다.
가상의 보에 M/EI도에 따라 하중이 재하되면, 반력은 $R_{L}={\frac {Ay}{L}}$ , $R_{R}={\frac {Ax}{L}}$ 이다.
처짐각 $(\theta )$ 은 $\theta _{L}={\frac {\Delta _{R}}{L}}={\frac {Ay}{L}},\theta _{R}={\frac {\Delta _{L}}{L}}={\frac {Ax}{L}}$

탄성하중법에 대한 핵심 정리

이게 모멘트면적법, 탄성하중법에 대한 핵심임!

단순보 임의 점에서 탄성곡선의 처짐각 $(\theta )$ (양쪽 지점을 현으로 하였을 때 측정한 값)은 M/EI도가 하중으로 작용하는 보에서 그 점의 전단력과 동일하다.
단순보 임의 점에서 탄성곡선의 처짐( $\Delta$ )(양쪽 지점을 현으로 하였을 때 측정한 값)은 M/EI도가 하중으로 작용하는 보에서 그 점의 모멘트와 동일하다.

17-4

D점 처짐각, 수직처짐? EI는 일정

곡률도(EI는 편의상 생략함.)만큼이 분포하중으로 보고 반력부터 계산한다.

${\begin{aligned}V_{A}&={\frac {1}{2}}\times {\frac {Pl}{4}}\times {\frac {l}{2}}\\&={\frac {Pl^{2}}{16}}\\\end{aligned}}$

D점 처짐각은 곡률도만큼 분포하중이 작용할 때 D점에서 전단력과 동일

${\begin{aligned}\theta _{D}&=V_{A}-{\frac {1}{2}}\times {\frac {Pl}{8}}\times {\frac {l}{4}}\\&={\frac {Pl^{2}}{16}}-{\frac {1}{2}}\times {\frac {Pl}{8}}\times {\frac {l}{4}}\\&={\frac {3Pl^{2}}{64}}\\\end{aligned}}$

D점 수직처짐은 곡률도만큼 분포하중이 작용할 때 D점에서 모멘트와 동일

${\frac {Pl^{2}}{16}}\times {\frac {l}{4}}+M={\frac {Pl^{2}}{64}}\times {\frac {l}{12}}$

${\begin{aligned}M&=Pl^{3}\left({\frac {1}{64\times 12}}-{\frac {1}{16\times 4}}\right)\\&=Pl^{3}\times \left(-{\frac {11}{768}}\right)\\\end{aligned}}$

14-1, 16-4

A점의 처짐각은? EI는 일정하다.

탄성하중법을 쓸 것이다. 먼저 반력을 구하고, 휨모멘트를 구한다음 EI로 나눈 값만큼을 하중으로 재하시킨 탄성하중도를 그린다.

$\sum M_{B}=0$

$M_{B}=V_{A}\cdot l$

$V_{A}={\frac {M_{B}}{l}}$

$\sum M_{B}=0$

$V_{A}\times l={\frac {M_{B}l}{2EI}}\times {\frac {l}{3}}$

$V_{A}={\frac {M_{B}l}{6EI}}$

A점 처짐각은 A점에서의 전단력과 같다. A점 전단력은 V_A이므로

$\theta _{A}={\frac {M_{B}l}{6EI}}$

공액보법

♣♣♣

원 구조에서 모멘트도를 구한 뒤, EI로 나눈 곡률도만큼 탄성하중을 원 구조의 공액보에 재하하여 처짐, 처짐각을 계산^[6]

Real support vs Conjugate support^[7]
Real beam		Conjugate beam
Fixed support		Free end
$v=0$ $\theta =0$		${\overline {M}}=0$ ${\overline {Q}}=0$
Free end		Fixed support
$v\not =0$ $\theta \not =0$		${\overline {M}}\not =0$ ${\overline {Q}}\not =0$
Hinged support		Hinged support
$v=0$ $\theta \not =0$		${\overline {M}}=0$ ${\overline {Q}}\not =0$
Middle support		Middle hinge
$v=0$ $\theta$ :continue		${\overline {M}}=0$ ${\overline {Q}}$ :continue
Middle hinge		Middle support
$v$ :continue $\theta$ :discontinue		${\overline {M}}$ :continue ${\overline {Q}}$ :discontinue

Examples of conjugate beam^[7]
Real beam		Conjugate beam
Simple beam
Cantilever beam
Left-end Overhanging beam
Both-end overhanging beam
Gerber's beam (2 span)
Gerber's beam (3 span)

00, 16-1 기출

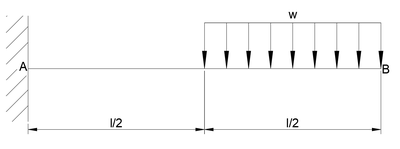
최대처짐각 θ_B를 구하시오.

반력계산

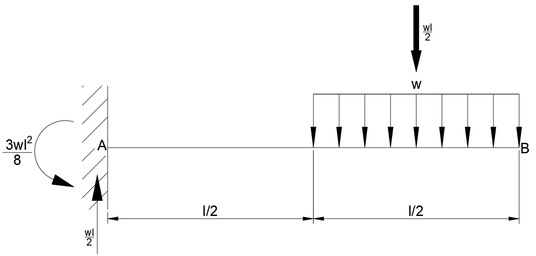
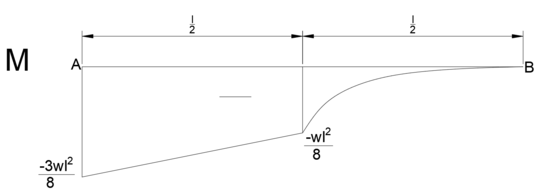
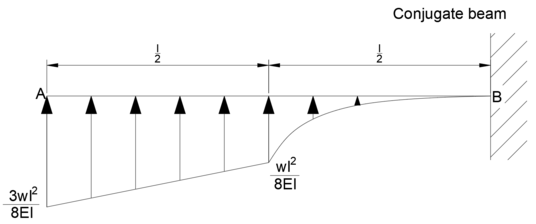
A에서 B까지 탄성하중도의 면적을 구하면 B에서의 최대처짐각이다.

사다리꼴 면적 + 포물선 제외 부분 면적하면 된다.

${\frac {wl^{3}}{8EI}}+{\frac {1}{3}}\times {\frac {l}{2}}\times {\frac {wl^{2}}{8EI}}={\frac {7wl^{3}}{48EI}}$

가상일의 방법

♣♣♣ 14-3, 15-1, 17-4, 18-1

구하고자 하는 점에 가상 단위 하중 1을 작용시켜 처짐을 구하는 방법.

$y_{x}=\int _{0}^{l}{\frac {M\cdot m}{EI}}dx$

처짐각을 구하고자 한다면 가상 단위 모멘트 1을 작용시켜야 된다. 처짐각 계산은 모멘트면적법이 편함.

Product Integral

$\int _{0}^{L}m_{1}m_{2}dx={\frac {L}{6}}[a(2c+d)+b(2d+c)]$

16-1

B점의 수평변위는? EI는 일정.

M, m을 찾는다.

M=-P\times 2r=-2Pr

m=-1\times x=-x

{\begin{aligned}\Delta &={\frac {1}{EI}}\int _{0}^{h}2Prxdx\\&={\frac {2Pr}{EI}}\int _{0}^{h}xdx\\&={\frac {Prh^{2}}{EI}}\end{aligned}}

암기해야할 변형값

♣♣♣ 14-2, 14-3, 16-2, 18-1, 18-3, 19-1, 19-3

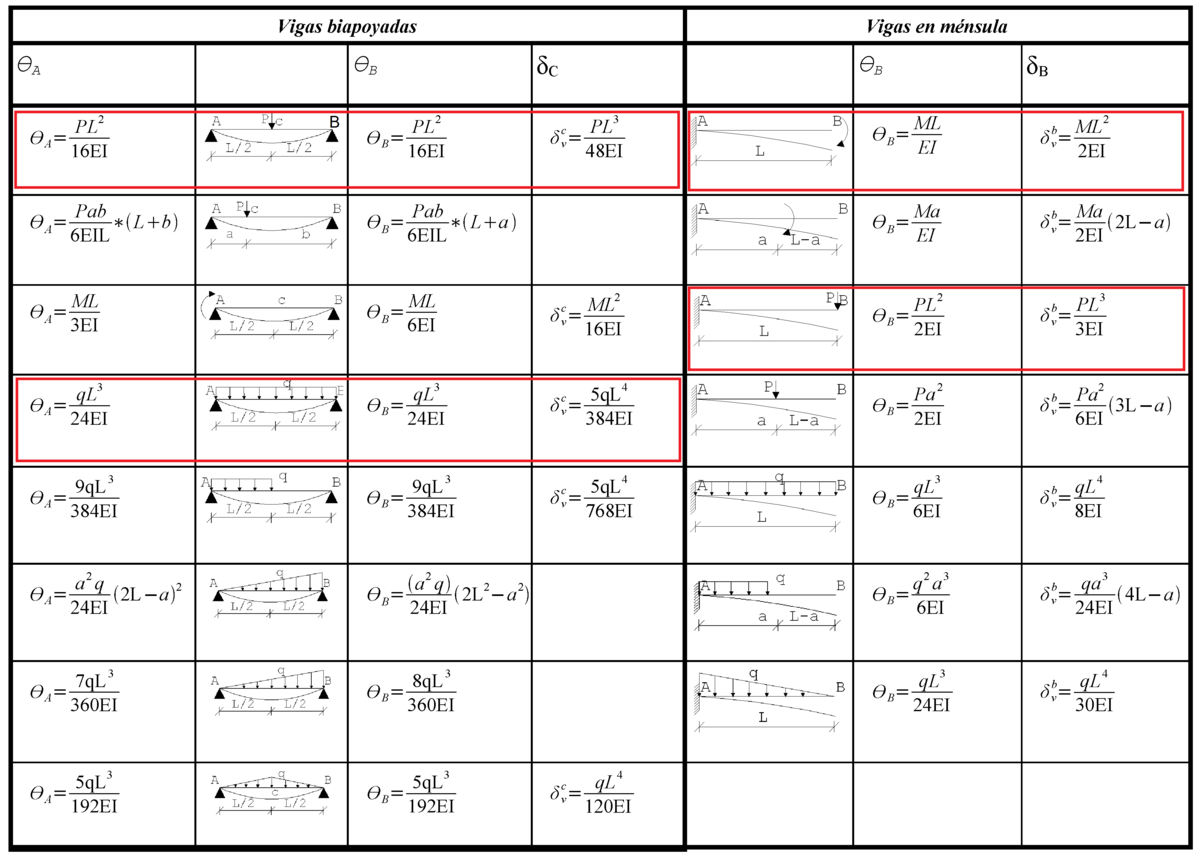
확실히 못 외우겠으면 그냥 계산하는 것도 나쁘지 않은 듯. 시간 남는다면.

19-2

중앙점 처짐 δ=0이 되도록 양쪽 지점에 모멘트 M을 작용시키려고 한다. M을 P, L로 나타내면?

δ는 암기한 값을 쓰거나 정 안 되면 계산해서 구한다.

\delta ={\frac {PL^{3}}{48EI}}

양쪽 지점에 모멘트를 가한 것에 의해 발생하는 변위가 위 δ와 상쇄되면 된다.

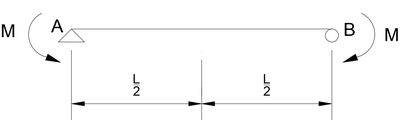
모멘트도를 그리고, M을 제거한 단순보의 변위를 구하고자 하는 점에 단위하중을 재하한 가상계의 모멘트도 m을 구한다. 변위일치법을 이용해 M에 의한 변위 Δ 계산

${\begin{aligned}EI\Delta &=2\times {\frac {1}{6}}\times {\frac {L}{2}}\left({\frac {L}{4}}(M+2M)\right)\\&={\frac {ML^{2}}{8}}\\\end{aligned}}$

혹은 더 간단한 방법으로, 공액보법을 쓴다. 단순보(공액보)에 ${\frac {M}{EI}}$ 의 등분포 탄성하중을 재하하고, 중앙점 처짐량은 중앙점 휨모멘트와 같으므로,

$\Delta ={\frac {{\frac {M}{EI}}L^{2}}{8}}={\frac {ML^{2}}{8EI}}$

$\Delta =\delta$ 이므로

${\frac {ML^{2}}{8EI}}={\frac {PL^{3}}{48EI}}$

$\therefore M={\frac {PL}{6}}$

02-1, 08-1, 12-1, 12-3, 15-2, 16-2

w = 1tf/m, δ = 1cm, $EI=2.0\times 10^{12}kg\cdot cm^{2}$ 일 때 가운데 지점의 수직반력 R_c는 얼마가 생기는가?

분포하중에 의한 처짐값(암기)

${\frac {5wL^{4}}{384EI}}$

수직반력을 집중하중이라고 봤을 때 처짐을 상쇄하는 변위량(암기하든, 탄성하중법으로 구하든)

${\frac {R_{c}\cdot L^{3}}{48EI}}$

${\frac {5wL^{4}}{384EI}}-{\frac {R_{c}\cdot L^{3}}{48EI}}=0.01m$

${\frac {5\times 1000kgf\times 20^{4}m^{4}}{384\times 2.0\times 10^{8}kg\cdot m^{2}}}-{\frac {R_{c}\cdot 20^{3}m^{3}}{48\times 2.0\times 10^{8}kg\cdot m^{2}}}=0.01m$