토목기사 요약/수리수문학/정수역학

출제 기준

2019-2021

압력의 정의
정수압 분포
정수력
부력

정수압의 원리

정수 중에서 전단응력은 0이다.(00)

99

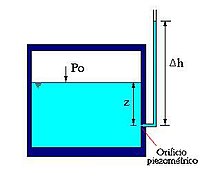
정수압 강도 1kg/cm²을 압력수두로 나타내시오.

풀이

$p=\gamma h$ 이므로

$h={\frac {p}{\gamma }}={\frac {1000g/cm^{2}}{1g/cm^{3}}}=1000cm=10m$

92

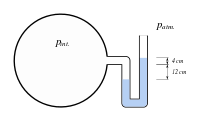
물이 채워진 용기가 있다. A점이 표준 대기압을 받고 있을 때, B점의 절대 압력은?

풀이

B점이 표준 대기압을 받는 수면보다 위에 있다는 건 압력이 그만큼 더 작다는 뜻이다. 따라서 표준대기압에서 물기둥만큼의 압력을 빼줘야 한다.

${\begin{aligned}p=-\gamma h+p_{atm}&=-1t/m^{3}\times 5m+10.33t/m^{2}\\&=0.533kg/cm^{2}\\\end{aligned}}$

압력 측정

액주계: 관 내 압력 재는 도구
피에조미터: 정수압 측정(90)
마노미터 : 압력 측정 (94)

피에조미터
마노미터

16-4

h = 0.5m일 때 A, B 사이 압력차는? 수은 비중은 13.5

$P_{A}+0.5\times 9.8=P_{B}+0.5\times 13.5\times 9.8$

$P_{A}-P_{B}=0.5\times 12.5\times 9.8=61.25kN/m^{2}$

01

A/a = 1000, L/l = 8, P = 10kg일 때 Q힘은?

풀이

파스칼의 법칙에서 ${\frac {Q}{A}}={\frac {G}{a}}$

$Gl=PL$ 이므로

$Q={\frac {A}{a}}\times {\frac {PL}{l}}=80000kg=80t$

02

바닥면 전수압은?

풀이

중간에 형태가 변해도 바닥면 넓이만으로 계산함.

${\begin{aligned}P=\gamma hA&=1g/cm^{3}\times 12cm\times {\frac {\pi \times 8^{2}cm^{2}}{4}}\\&=603g\\\end{aligned}}$

수중 물체에 작용하는 전수압

♣♣02

흐르지 않는 물에 잠긴 평판에 작용하는 전수압은 도심의 수압에 평판 면적을 곱해 구한다.
수심과 단면적이 같으면 전수압도 일정
전수압: 정수압에 면적 곱한 것[kg]
정수압: 정수 중 물의 압력 강도[kg/cm²]
수면에 평행한 평면에 작용하는 전수압은 평면의 도심에 작용

연직 평면에 작용하는 전수압

13-1

전면적 A에 작용하는 수압(h_c: 수면에서 도심까지의 깊이)

$F_{w}=\gamma _{w}{\color {red}h_{c}}A$

전수압의 작용점

$h_{p}=h_{c}+{\frac {I_{c}}{h_{c}A}}$

$I_{c}$ : 도심에 대한 단면이차모멘트

10, 20-1+2

두 변의 길이가 3m인 직각이등변 삼각형의 한 변을 자유표면에 두면 자유표면으로부터 정수압의 작용점은?

풀이

정수압 작용점 $h_{p}=h_{c}+{\frac {\frac {bh^{3}}{36}}{h_{c}A}}=1.5m$

95

오른쪽 그림에서 단면에 작용하는 힘의 작용점은 AB로부터 수평으로 몇 m 떨어진 곳에 있는가?

풀이

ABCG, GDEF 단면으로 구분해서 각각의 전수압을 계산한다.

ABCG: $P_{1}=1t/m^{3}\times 1m\times 2m^{2}=2t$

GDEF: $P_{2}=1t/m^{3}\times 0.5m\times 1m^{2}=0.5t$

전단면: 2 + 0.5 = 2.5t

AB 면에서 각 단면 작용점까지 거리는

ABCG: ${\frac {AG}{2}}$

GDEF: $AG+{\frac {GF}{2}}$

이제 A에서 모멘트를 취한다.

$Px=P_{1}\times {\frac {AG}{2}}+P_{2}\times \left(AG+{\frac {GF}{2}}\right)$

$2.5t\times x=2t\times 0.5m+0.5t\times 1.5m$

x = 0.7m

경사진 평면에 작용하는 전수압

전수압

${\begin{aligned}F_{w}&=\gamma _{w}{\color {red}h_{c}}A\\&=\gamma _{w}y_{c}\sin \theta A\\\end{aligned}}$

O점에서 작용점 위치까지 경사깊이

$y_{p}=y_{c}+{\frac {I_{cx}}{y_{c}A}}$

$I_{cx}$ : Ox축에 평행하면서 단면의 도심을 지나는 축에 대한 단면이차모멘트

수면에서 작용점 위치까지 연직깊이

$h_{p}=y_{p}\sin \theta$

참고 자료

임진근 외 (2015). 《토목기사 필기 - 수리수문학》. 성안당.
김경호 (2010). 《수리학》. 한티미디어.

곡면에 작용하는 전수압

♣98, 12-3, 14-1, 16-4

수평분력 P_H : 연직면에 투영한 면에 작용하는 전수압
수직분력 P_V : 곡면을 저면으로 하는 수면까지 수주 무게(투영면이 중복되는 부분은 빼줘야 함)
합력 $P={\sqrt {{P_{H}}^{2}+{P_{V}}^{2}}}$
작용점: w:바리뇽의 정리로 구함

96

길이방향으로 1m인 원통이 물을 막고 있다. 원통의 곡면에 작용하는 전수압을 구하시오.

풀이

수평수압은 연직방향으로 투영시킨 면에 작용하는 전수압과 같다.

P_{H}=1t/m^{3}\times 2m^{2}\times 1m=2t

수직수압은 곡면을 저면으로 하는 수주의 수면까지의 무게와 같다. 이때 중첩되는 부분은 계산에서 제외한다.

{\begin{aligned}P_{V}&=1t/m^{3}\times \left({\frac {\pi }{4}}\times 2^{2}m^{2}\times {\frac {1}{2}}\times 1m\right)\\&={\frac {\pi }{2}}t=1.57t\\\end{aligned}}

전수압은 다음과 같이 구한다.

P={\sqrt {{P_{H}}^{2}+{P_{V}}^{2}}}=2.54t

11, 20-1+2

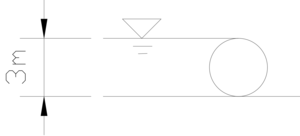
길이 8m인 드럼게이트에 작용하는 전수압이 수문에 작용하는 지점 수심을 구하시오.

풀이

수평, 연직 분력을 각각 먼저 계산하면 P_H = 36t, P_V = 9πt.

원의 중심 O에서 $x=1.5\cos \theta ,\quad y=1.5\sin \theta$

$\sum M_{O}=0$

P_H y = P_V x

$36\times 1.5\sin \theta =9\pi \times 1.5\cos \theta$

$\tan \theta ={\frac {9\pi \times 1.5}{36\times 1.5}}$

θ = 38.15도

수문의 작용점까지 수심

${\begin{aligned}h_{c}&=1.5m+y\\&=1.5+1.5\sin \theta \\&=2.43m\end{aligned}}$

예제

길이 3m인 반원통 물체가 물에 잠겨있다. 반원통에 작용하는 물에 의한 합력의 O점에 관한 모멘트를 계산하시오.

풀이

$P_{V}=\gamma _{w}V=1t/m^{3}\times \left({\frac {1}{2}}\times {\frac {\pi \times 2^{2}}{4}}m^{2}\times 3m\right)=1.5\pi t$

연직수압은 O점에서 0.4244r 떨어진 곳에 작용하므로

M = 4.71t×0.4244×1 = 2t·m

원관 수압

♣93, 00, 02 / 응용역학 13-2 / 상수도 96, 19-3

$pD=\sigma _{ta}\cdot 2t$

p: 수압

σ_ta: 허용 인장 응력

t: 강관 두께

참고 서적

James M. Gere & Barry J. Goodno. 《SI 재료역학》 8판. 센게이지 러닝 코리아. 635쪽.

부력

♣♣♣ 부력: 수중 부분 체적만큼의 물의 무게.

90

4×5×1m³ 목재판에 2000kg의 하중이 놓여 있다. 목재 비중이 0.5라고 하면 목재판이 물에 잠기는 체적은?

풀이

${\begin{aligned}B&=W+2000kg\\&=20m^{3}\times 0.5t/m^{3}+2000kg\\&=10000kg+2000kg=12t\end{aligned}}$

B = $\gamma _{w}V=1t/m^{3}\times 4\times 5m^{2}\times d$

d = 12 / 20 = 0.6m

$\therefore V=20\times 0.6m^{3}=12m^{3}$

98, 유사 13-1, 18-3

떠 있는 부분이 102.45m³인 빙산의 전체적을 구하시오. 빙산의 비중은 0.92, 해수 비중은 1.025이다.

풀이

V_t: 빙산 전체적

V: 떠 있는 부분 체적

V': 잠긴 부분 체적

W = B

0.92 V_t = 1.025 V' = 1.025 (V_t - V)

$V_{t}={\frac {1.025V}{1.025-0.92}}=1000m^{3}$

부체의 안정

부심(center of buoyancy, C): 배제 체적 물의 무게 중심
경심(metacenter, M): 부력 작용선과 부체 중심선의 교점. MG는 경심고(metacentric height)
경심고 $MG={\frac {P\cdot L}{W\cdot \tan \theta }}$ $MG={\frac {P\cdot L}{W\cdot \tan \theta }}$ (부체에 대한 우력모멘트 이용해서 유도) (02)
- P : 움직일 하중의 크기
- L : 하중을 선박 대칭축 방향에 직각이 되게 이동시킨 거리
- W : 선박 배수 용량
- tan θ : 기울어진 각도의 탄젠트값
- $MG={\frac {I_{x}}{V}}-GC>0$ $MG={\frac {I_{x}}{V}}-GC>0$ 이면 안정, < 0이면 불안정 (97)
  - I_x : 부양면의 최소 단면 2차 모멘트
  - V : 부체의 수중 부분 체적
  - GC : 부심에서 중심까지 거리