- 92, 13-2, 17-4
 그림에서 RA 크기를 W로 나타내시오.
그림에서 RA 크기를 W로 나타내시오.
- 풀이
아래쪽 반력의 작용점에서 모멘트의 합이 0임을 이용한다.



♣♣
한 점에 작용하는 두 힘의 합성 : 힘의 사변형 법칙, 삼각형 법칙 사용.

♣♣♣
95, 00 기출
 1600과 600 힘의 합력은 R과 같다. R의 크기는?
1600과 600 힘의 합력은 R과 같다. R의 크기는?
풀이
1600, 600을 R의 좌표계(?)에 맞게 분해해준 뒤, 구하려고 하는 방향의 힘만 더해서 구해주면 됨.

84, 87, 96 기출, 14-2 유사
 두 부재가 받는 힘은? 오른쪽 끝에서 당기는 힘은 1000이다.
두 부재가 받는 힘은? 오른쪽 끝에서 당기는 힘은 1000이다.
풀이
위의 부재는 인장되고 아래 부재는 압축될 것이다. 여기에 따라 가상의 힘 PA, PB를 도입한다. PA는 횡방향 힘만 있으므로 그냥 두고, PB는 대각선으로 작용하니까 수직, 수평방향으로 분할한다. 그림으로 나타내면 다음과 같다.

이제 가로, 세로 방향 힘의 평형을 이용해서 PA, PB를 계산. PA = 1732(인장), PB = 2000(압축)
91, 95, 18-1 기출
 A 부재 축방향력은?
A 부재 축방향력은?
풀이
A에 작용하는 축력을 P라고 하고 P를 가로, 세로로 분해한다. O점에서 모멘트 합을 취해보면


90
 D가 받는 힘은?
D가 받는 힘은?
풀이
ΣV = 0이므로 D = 0
14-2, 17-4

AB부재가 받는 힘의 크기를 구하시오.
B에서 수평반력을 우측으로 가정하고,


HB = - 2533t (처음 가정과 반대방향인 왼쪽방향으로 2533t)


2533 : 4 = x : 5

92, 93, 99, 01, 16-2
 P를 a와 W로 나타내시오.
P를 a와 W로 나타내시오.
풀이


15-2

BC 케이블에 걸리는 장력은?
겉보기에 직각삼각형으로 보인다고 직각삼각형으로 보고 풀면 안 된다!! 귀찮아도 직접 확인해야함.






대입해서 T2를 구하면

19-2
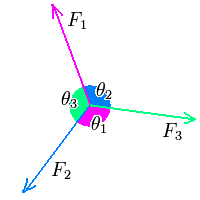
Lami's theorem.


 1600과 600 힘의 합력은 R과 같다. R의 크기는?
1600과 600 힘의 합력은 R과 같다. R의 크기는?
 두 부재가 받는 힘은? 오른쪽 끝에서 당기는 힘은 1000이다.
두 부재가 받는 힘은? 오른쪽 끝에서 당기는 힘은 1000이다.





























