토목공학/응용역학/재료의 역학적 성질

출제 기준

2019-2021

응력과 변형률
탄성계수

응력

평면응력 상태 임의 경사면 응력

♣♣♣ 91, 13-3

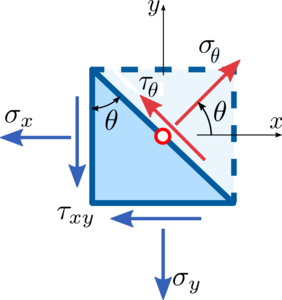
경사면 수직응력

$\sigma _{\theta }={\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\theta +\tau _{xy}\sin 2\theta$

경사면 전단응력^[1]

$\tau _{\theta }={\color {red}-}{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\theta +\tau _{xy}\cos 2\theta$

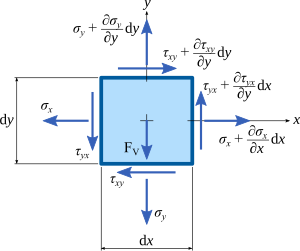
평면응력 상태
평면 응력 상태의 임의 경사면 응력

평면응력 상태 주응력, 작용면

θ가 변할 때,

주응력 : $\sigma _{\theta }$ 의 최대, 최솟값
주 전단응력 : $\tau _{\theta }$ 의 최대, 최솟값

♣♣♣ 96, 00

$\sigma _{max,min}=\sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+{\tau _{xy}}^{2}}}$

주응력면

$\tan 2\theta _{p}={\frac {\tau }{\frac {\sigma _{x}-\sigma _{y}}{2}}}$

평면응력 상태 주 전단응력, 작용면

주 전단응력 : 모어원 생각

${\begin{aligned}\tau _{max,\ min}&=\pm {\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+{\tau _{xy}}^{2}}}\\&=\pm {\frac {\sigma _{max}-\sigma _{min}}{2}}\end{aligned}}$

93

주전단응력면은 서로 직교
주응력면과 주전단응력면은 45도의 차이가 있다.
주응력면에서의 전단응력은 0이다.
주전단응력면에서의 주응력은 0이 아니다.

평면응력 상태 식들을 외웠다면 아래에 적은 다른 상태의 식들을 유도할 수 있다.

1축응력 상태 경사면 응력

82, 83, 87, 92, 97, 13-3

경사면 수직응력

${\begin{aligned}\sigma _{\theta }&={\frac {\sigma _{x}+0}{2}}+{\frac {\sigma _{x}-0}{2}}\cos 2\theta +0\\&={\frac {1}{2}}\sigma _{x}(1+\cos 2\theta )\\&={\frac {1}{2}}\sigma _{x}({\cancel {1}}+2\cos ^{2}\theta -{\cancel {1}})\\&=\sigma _{x}\cdot \cos ^{2}\theta \\\end{aligned}}$

경사면 전단응력^[2]

$\tau _{\theta }={\color {red}-}{\frac {\sigma _{x}}{2}}\sin 2\theta ={\color {red}-}\sigma _{x}\cdot \sin \theta \cdot \cos \theta$

1축응력 상태 주응력

77, 78, 83

경사면 주 전단응력

$\tau _{max,min}=\pm {\frac {1}{2}}{\sqrt {{\sigma _{x}}^{2}}}=\pm {\frac {\sigma _{x}}{2}}$

2축응력 상태 경사면 응력

90 (토질 96, 98, 00, 01, 03, 06) ♣♣♣

경사면 수직응력

${\begin{aligned}\sigma _{\theta }&={\frac {\sigma _{x}+\sigma _{y}}{2}}+{\frac {\sigma _{x}-\sigma _{y}}{2}}\cos 2\theta \\&=\sigma _{x}\cos ^{2}\theta +\sigma _{y}\sin ^{2}\theta \\\end{aligned}}$

(토질 01, 02, 04, 06, 08, 10 ♣♣♣)

경사면 전단응력^[3]

${\begin{aligned}\tau _{\theta }&=-{\frac {\sigma _{x}-\sigma _{y}}{2}}\sin 2\theta \\&=-(\sigma _{x}-\sigma _{y})\sin \theta \cos \theta \end{aligned}}$

경사면 주 전단응력

$\tau _{max,min}=\pm {\frac {\sigma _{x}-\sigma _{y}}{2}}$

비틀림 모멘트에 의한 전단 응력

원형단면

♣♣ 00, 14-1, 15-3, 16-3, 17-4, 18-1

$\tau ={\frac {Tr}{J}}$

J : 비틀림 상수.
r : 바깥쪽 반지름

비틀림상수 J는 원형 단면의 경우엔 단면 2차 극모멘트

${\begin{aligned}J=I_{P}&=I_{x}+I_{y}\\&=2\times {\frac {\pi d^{4}}{64}}={\frac {\pi d^{4}}{32}}\\\end{aligned}}$

얇은 직사각형 관

12-1, 15-2

두께가 얇은 관의 비틀림 공식

$\tau ={\frac {T}{2t\cdot A_{m}}}$

T : 비틀림 우력[FL]
t : 관의 최소두께
A_m : 그림 참조

조합응력

97, 99, 17-4

1, 2의 단면적이 같다고 하면 1에 발생하는 힘 P₁?

1) $\sigma =E\epsilon ={\frac {P}{A}}$

\sigma _{1}=E_{1}\epsilon _{1},\ \sigma _{2}=E_{2}\epsilon _{2}

P=\sigma \cdot A=\sigma _{1}\cdot A_{1}+\sigma _{2}\cdot A_{2}=P_{1}+P_{2}

2) 재료가 달라도 조합부재의 경우 변형은 같다.

\epsilon _{1}=\epsilon _{2}

{\frac {\sigma _{1}}{E_{1}}}={\frac {\sigma _{2}}{E_{2}}}

\sigma _{1}={\frac {E_{1}}{E_{2}}}\sigma _{2}

\sigma _{2}={\frac {E_{2}}{E_{1}}}\sigma _{1}

3)

${\begin{aligned}P&=\sigma _{1}A_{1}+{\frac {E_{2}}{E_{1}}}\sigma _{1}A_{2}\\&=\sigma _{1}\left(A_{1}+{\frac {E_{2}}{E_{1}}}A_{2}\right)\\\end{aligned}}$

${\begin{aligned}\sigma _{1}&={\frac {P}{A_{1}+{\frac {E_{2}}{E_{1}}}A_{2}}}\\&={\frac {P}{A\left(1+{\frac {E_{2}}{E_{1}}}\right)}}\quad (\because A_{1}=A_{2})\\\end{aligned}}$

${\begin{aligned}P_{1}=\sigma _{1}A_{1}&={\frac {P}{1+{\frac {E_{2}}{E_{1}}}}}\\&={\frac {E_{1}}{E_{1}+E_{2}}}P\\\end{aligned}}$ 결론만 외우자.

열응력

♣♣

$\sigma =E\cdot \epsilon =E\cdot \alpha (t_{2}-t_{1})$

α : 선팽창계수(/°C)

원환응력

토목공학/수리학·수문학·상하수도 공학/정수역학#원관 수압 참고!

변형

푸아송 비

82, 83: 푸아송 수는 υ의 역수

♣♣♣

$\nu =-{\frac {\epsilon '}{\epsilon }}$

$\epsilon '$ 은 가로방향 변형도, $\epsilon$ 은 축방향 변형도

3축 응력 변형률

99

$\epsilon _{x}={\frac {1}{E}}(\sigma _{x}-\nu (\sigma _{y}+\sigma _{z}))$

$\epsilon _{y}={\frac {1}{E}}(\sigma _{y}-\nu (\sigma _{x}+\sigma _{z}))$

$\epsilon _{z}={\frac {1}{E}}(\sigma _{z}-\nu (\sigma _{x}+\sigma _{y}))$

2축응력 상태의 변형률

96

3축응력 상태 변형률을 이용하면 유도 가능.

$\epsilon _{x}={\frac {1}{E}}(\sigma _{x}-\nu \sigma _{y})$

$\epsilon _{y}={\frac {1}{E}}(\sigma _{y}-\nu \sigma _{x})$

체적 변형률

♣♣♣14-1

${\begin{aligned}{\frac {\Delta V}{V}}&=\epsilon _{x}+\epsilon _{y}+\epsilon _{z}\\&={\frac {1-2\nu }{E}}(\sigma _{x}+\sigma _{y}+\sigma _{z})\\\end{aligned}}$