토목공학/응용역학/보의 응력

합성단면 중립축

두 종류 재료로 된 직사각형 보의 중립축 구하기. 단면 상단에서 중립축까지 거리를 c, 중립축에서 각 단면 도심까지 거리를 y₁, y₂라 할 때

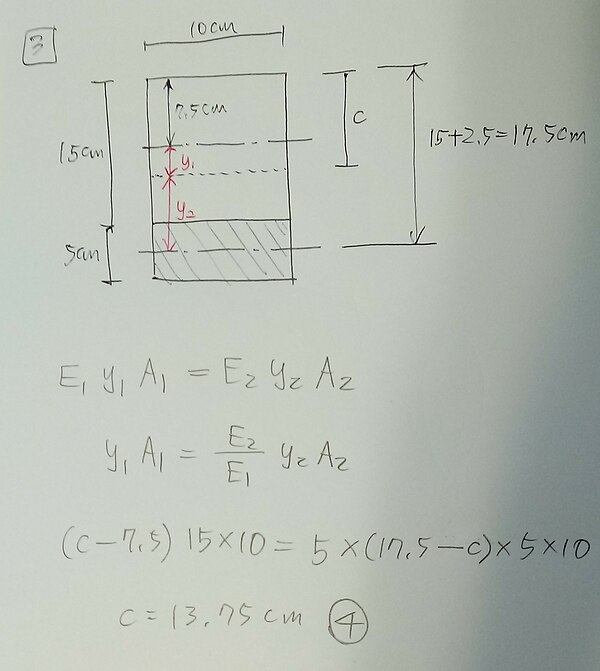
이렇게도 표현 가능. 최상단으로부터 각 단면 도심까지 거리를 ${\overline {y_{1}}},\ {\overline {y_{2}}}$라 한다면,

$(E_{1}A_{1}+E_{2}A_{2})c=E_{1}{\overline {y_{1}}}A_{1}+E_{2}{\overline {y_{2}}}A_{2}$

$\therefore c={\frac {E_{1}{\overline {y_{1}}}A_{1}+E_{2}{\overline {y_{2}}}A_{2}}{E_{1}A_{1}+E_{2}A_{2}}}$

---

참고서적

• 전찬기 외 (2015). 《토목기사 필기 응용역학》. 성안당. 261쪽. 
• Gere & Goodno. 《SI 재료역학》 8판. 480-483쪽. 

휨응력

• 정의 : 휨모멘트에 의해 부재 한 단면 위에 일어나는 수직응력(96)

♣♣♣ 07-2, 14-2, 15-1, 15-2, 17-4, 18-1

$\sigma ={\frac {M}{I}}y$

전단응력

♣♣♣ 14-2, 14-3, 15-2, 17-2, 17-4, 18-1, 18-3

$\tau ={\frac {VG}{Ib}}$

G : 보 단면에서 τ를 구하려는 위치 바깥쪽 단면적을 중립축에 대해 1차 모멘트 취한 값.

b : 최대 전단응력 구하려면 최소폭 씀(83, 00)

---

14-3, 17-2

우측 그림과 같은 단면에 전단력 60t이 작용할 때 최대 전단응력을 구하시오. 치수 단위는 cm이다.

---

V = 60000 kg

G 계산하는 거 보면 중립축에 대한 전단응력을 구하는 듯...

${\begin{aligned}G&=A_{1}{\overline {y_{1}}}+A_{2}{\overline {y_{2}}}\\&=(30\times 10)\times (15+5)+(15\times 10)\times 7.5\\&=7125cm^{3}\end{aligned}}$

만약에 플랜지와 복부 경계면에서 최대전단응력을 구하라고 한다면 위에 구한 G에서 $A_{2}{\overline {y_{2}}}$는 제외하고 계산함(83)

${\begin{aligned}I&={\frac {30\times 50^{3}}{12}}-2\times {\frac {10\times 30^{3}}{12}}\\&=267500cm^{4}\\\end{aligned}}$

b = 10cm (최소폭)

${\begin{aligned}\tau &={\frac {60000\times 7125}{267500\times 10}}\\&=160kg/cm^{2}\\\end{aligned}}$

---

90, 97

• B : 휨응력 최대
• D : 휨응력 최소
• A : 전단응력 0
• C : 전단응력만 존재. 휨응력 0

최대 전단 응력

직사각형 단면(07-2, 14-2, 19-1, 19-2)

$\tau _{max}={\frac {3}{2}}{\frac {V}{A}}=1.5\tau _{mean}$

원형 단면(16-2)

$\tau _{max}={\frac {4}{3}}{\frac {V}{A}}$

비대칭 휨과 전단중심

전단 흐름 = 전단류(shear flow)

♣♣

$f={\frac {VG}{I}}$

못 박는 문제(10-1, 16-4)

$f={\frac {VG}{I}}={\frac {n\cdot F}{s}}$

• n : 못 박는 줄수
• F : 못 하나가 받을 수 있는 전단력
• s : 못 간격

전단 중심 : 단면이 받는 전단력 합력점 위치. 1축 대칭 단면은 대칭축상에 있음.(도심 아님!)