지중응력 분포

상위 문서 : 토질역학

흙의 무게로 인한 지반 내 응력

예제 기사 시험 출제되는데 암기보단 이해임

모관현상에 의해 두번째 층까지 포화됨. 바닥면 유효응력은?

---

${\begin{matrix}\sigma &=&Z\cdot \gamma _{sat}+h_{2}\cdot \gamma _{sat}+h_{1}\cdot \gamma _{1}\\&=&\gamma _{sat}(Z+h_{2})+\gamma _{1}h_{1}\end{matrix}}$

$u=\gamma _{w}Z+\gamma _{w}h_{2}-h_{2}\cdot \gamma _{w}=Z\gamma _{w}$

${\begin{matrix}{\bar {\sigma }}=\sigma -u&=&\gamma _{sat}(Z+h_{2})+\gamma _{1}h_{1}-Z\gamma _{w}\\&=&Z\cdot \gamma _{sub}+\gamma _{sat}\cdot h_{2}+\gamma _{1}h_{1}\\&=&(Z+h_{2})\gamma _{sub}+\gamma _{1}h_{1}+\gamma _{w}h_{2}\end{matrix}}$

지하수위 이하의 흙은 부력을 받으니까 $\gamma _{sub}=\gamma _{sat}-\gamma _{w}$의 개념을 이용하지만, 지하수위 위의 흙은 포화되었더라도 γ_sub가 아닌 γ_sat을 그대로 쓴다.

지표 하중 재하로 인한 지중응력 증가

기본적으로 집중하중(point load)에 의한 응력 증가량, 선하중(line load)에 의한 응력 증가량을 가지고 나머지 경우들이 파생됨. 좌표계는 Cartesian, 원통형 좌표계 두 개가 각각 이용됨.

부호 규약

여기서 쓰는 부호규약은 구조역학과 정반대. 즉

• 수직응력은 압축이 +, 인장이 -
• 전단응력은 입자가 반시계방향 회전하면 +, 시계방향 회전하면 -

집중하중에 의한 응력 증가량

μ는 포아송비이다.

연직 응력 증가량 $\Delta \sigma _{z}=-{\frac {3P}{2\pi R^{2}}}\cos ^{3}\theta$

방사선 응력 증가량 $\Delta \sigma _{r}={\frac {P}{2\pi R^{2}}}(-3\cos \theta \sin ^{2}\theta +{\frac {1-2\mu }{1+\cos \theta }})$

접선 응력 증가량 $\Delta \sigma _{t}={\frac {P}{2\pi R^{2}}}(1-2\mu )(\cos \theta -{\frac {1}{1+\cos \theta }})$

전단 응력 증가량 $\Delta \tau =-{\frac {3P}{2\pi R^{2}}}\cos ^{2}\theta \sin \theta$

그림에서 $\cos \theta ={\frac {z}{R}}$, $R={\sqrt {r^{2}+z^{2}}}$이므로 연직응력증가량 $\Delta \sigma _{z}=-{\frac {3Pz^{3}}{2\pi R^{5}}}=-{\frac {3P}{2\pi }}{\frac {z^{3}}{(r^{2}+z^{2})^{5/2}}}=-{\frac {3P}{2\pi z^{2}\left[1+\left({\frac {r}{z}}\right)^{2}\right]^{\frac {5}{2}}}}$으로도 나타낼 수 있다.

원형 등분포하중에 의한 응력증가량

원형 등분포 하중에 의한 연직응력증가

반지름이 r₀인 원형 등분포하중에 의한 z 깊이에서의 연직응력증가량 q_z는 접촉압(contact pressure)을 $q_{0}={\frac {P}{A}}$라 할 때 다음과 같다. 이는 미소요소에 대한 집중하중에 의한 연직응력증가량 식을 적분하여 구한 것이다.

$q_{z}=q_{0}\left\{1-\left[1+\left({\frac {r_{0}}{z}}\right)^{2}\right]^{-{\frac {3}{2}}}\right\}$

Δτ_xz = 0

선하중에 의한 응력 증가량

선하중에 의한 연직응력증가

$\Delta \sigma _{z}={\frac {2qz^{3}}{\pi (x^{2}+z^{2})^{2}}}={\frac {2q}{\pi z\left[\left({\frac {x}{z}}\right)^{2}+1\right]^{2}}}$

$\Delta \sigma _{x}={\frac {2qx^{2}z}{\pi (x^{2}+z^{2})^{2}}}$

$\Delta \tau _{xz}={\frac {2qxz^{2}}{\pi (x^{2}+z^{2})^{2}}}$

대상등분포하중으로 인한 응력 증가량

대상등분포하중(strip load)이란 줄기초에 q/단위면적의 응력이 작용하는 것.

$\Delta \sigma _{z}={\frac {q}{\pi }}[\beta +\sin \beta \cdot \cos(\beta +2\delta )]$

$\Delta \sigma _{x}={\frac {q}{\pi }}[\beta -\sin \beta \cdot \cos(\beta +2\delta )]$

$\Delta \tau _{xz}={\frac {q}{\pi }}\sin \beta \cdot \sin(\beta +2\delta )$

예제1

간이법

간이법은 2:1법이라고도 부른다. 만약 지표면 위에 기초가 있는 게 아니라 지표면을 굴착해서 기초가 설치되었다면 굴착된 부분만큼의 응력감소와, 지하수의 부력에 의한 응력감소분을 P에서 빼주어야 한다.

$PBL=Q=\Delta \sigma _{z}(B+z)(L+z)$

$\Delta \sigma _{z}={\frac {PBL}{(B+z)(L+z)}}$

띠하중인 경우는

$\Delta \sigma _{z}={\frac {PB}{B+z}}$

모어원

$\sigma _{max,min}=\sigma _{1,2}={\frac {\sigma _{x}+\sigma _{y}}{2}}\pm {\frac {1}{2}}{\sqrt {(\sigma _{x}-\sigma _{y})^{2}+4{\tau _{xy}}^{2}}}$

• 토질역학에서 전단응력이 0인 세 개의 평면을 주응력면
• 3개 주응력 중 가장 큰 응력 : 최대주응력 σ₁
• 3개 주응력 중 가장 작은 응력 : 최소주응력 σ₃
• 나머지 응력 : σ₂

평면기점 예제

그림에서 $\theta =35^{\circ }$일 때 경사면에 작용하는 σ, τ를 구하시오.

• $\sigma _{1}=5.2kg/cm^{2}$
• $\sigma _{3}=1.2kg/cm^{2}$

---

극점

p-q 다이어그램

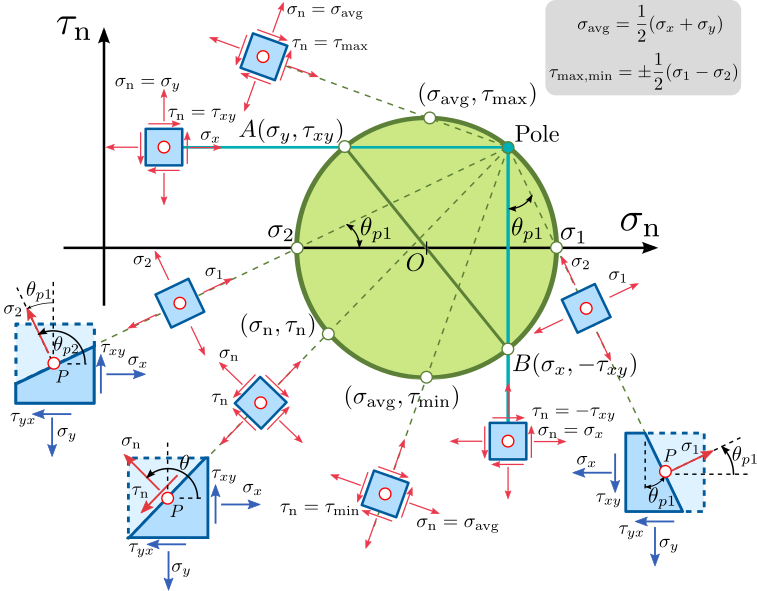
모어원의 정점을 연결한 선

하중 재하 전 상재압력

$p={\frac {\sigma _{v}+\sigma _{h}}{2}}={\frac {(1+K_{0})\sigma _{v0}}{2}}$

$q={\frac {\sigma _{v}-\sigma _{h}}{2}}={\frac {(1-K_{0})\sigma _{v0}}{2}}$

하중 재하 후 응력

${\begin{aligned}p&={\frac {(\sigma _{v0}+\Delta \sigma _{v})+(\sigma _{h0}+\Delta \sigma _{h})}{2}}\\&={\frac {\sigma _{v0}(1+K_{0})}{2}}+{\frac {\Delta \sigma _{v}+\Delta \sigma _{h}}{2}}\\\end{aligned}}$

${\begin{aligned}q&={\frac {(\sigma _{v0}+\Delta \sigma _{v})-(\sigma _{h0}+\Delta \sigma _{h})}{2}}\\&={\frac {\sigma _{v0}(1-K_{0})}{2}}+{\frac {\Delta \sigma _{v}-\Delta \sigma _{h}}{2}}\\\end{aligned}}$

p-q 다이어그램의 기울기를 나타내는 선이 K₀선.

$\beta ={\frac {1-K_{0}}{1+K_{0}}}$

초기 상재압력의 p, q값은 K₀선 상에 있다. 하중 재하 후 p, q 값은 K₀선을 벗어난다.

주의점 이인모 <<토질역학의 원리>> 예제 5.9 참조!! 전단응력이 있는 경우 q값이 항상 양(+)은 아니다!