자료 정보
진행 상황
교육 수준 대학교 강의 수준의 자료입니다.
과목 정보 공학 과목의 자료입니다.
자료 형식 문서형식 의 자료입니다.
압밀에 대한 설명은 위키백과의 압밀 참고.
토질역학 목차 : 토질역학
흙시료 건조 중량 120gf, 시료 초기높이 2.50cm, Gs =2.75, 시료 단면적 30cm2 일 때 e-log p 곡선을 그리시오.
압력 p (kgf/cm2 )
압밀 완료 시료 최종 높이 H(cm)
0
2.500
0.05
2.488
0.1
2.465
0.2
2.431
0.4
2.389
0.8
2.324
1.6
2.225
3.2
2.115
풀이 1. 공극 제외 흙시료 높이 Hs 계산
H
s
=
V
s
A
=
W
s
A
γ
s
=
W
s
A
G
s
γ
w
=
120
g
f
30
c
m
2
×
2.75
×
1
g
f
/
c
m
3
=
1.4545
c
m
{\displaystyle H_{s}={\frac {V_{s}}{A}}={\frac {W_{s}}{A\gamma _{s}}}={\frac {W_{s}}{AG_{s}\gamma _{w}}}={\frac {120gf}{30cm^{2}\times 2.75\times 1gf/cm^{3}}}=1.4545cm}
2. 공극만의 초기높이 Hv 계산
H
v
=
H
−
H
s
{\displaystyle H_{v}=H-H_{s}}
압력 p (kgf/cm2 )
압밀 완료 시료 최종 높이 H(cm)
Hs
Hv
e
=
H
v
H
s
{\displaystyle e={\frac {H_{v}}{H_{s}}}}
0
2.500
1.4545
1.04550
0.05
2.488
1.4545
1.03350
0.1
2.465
1.4545
1.01050
0.2
2.431
1.4545
0.97650
0.4
2.389
1.4545
0.93450
0.8
2.324
1.4545
0.86950
1.6
2.225
1.4545
0.77050
3.2
2.115
1.4545
0.66050
3. e 계산
압력 p (kgf/cm2 )
압밀 완료 시료 최종 높이 H(cm)
Hs
Hv
e
=
H
v
H
s
{\displaystyle e={\frac {H_{v}}{H_{s}}}}
0
2.500
1.4545
1.04550
0.71880
0.05
2.488
1.4545
1.03350
0.71055
0.1
2.465
1.4545
1.01050
0.69474
0.2
2.431
1.4545
0.97650
0.67136
0.4
2.389
1.4545
0.93450
0.64249
0.8
2.324
1.4545
0.86950
0.59780
1.6
2.225
1.4545
0.77050
0.52974
3.2
2.115
1.4545
0.66050
0.45411
가로축을 log 스케일로, 세로축을 e로 그래프를 그리면
Matlab 또는 GNU Octave로 계산하는 것은 Matlab/그래프#semilogx 를 참조.
Gs = 2.73, 초기 점토시료 두께 = 19.0mm, 최종순간 함수비 = 19.8%이고, 압밀시험결과가 다음과 같다고 하자.
압력(kPa)
0
54
107
214
429
858
1716
3432
0
24시간 후 다이얼게이지 읽음값(mm)
5.00
4.747
4.493
4.108
3.449
2.608
1.676
0.737
1.480
e - log σ' 그래프를 그리시오.
원래
H
s
=
W
s
A
G
s
γ
w
{\displaystyle H_{s}={\frac {W_{s}}{AG_{s}\gamma _{w}}}}
s 를 구하지만, 문제의 조건에서 알 수 있는 값은 Gs , γw (기지값)이므로 Ws , A를 몰라서 다른 방법으로 Hs 를 구해야 한다.
흙의 삼상관계를 생각하여 Hs 를 구해야 한다.
포화된 점토시료(S = 1)에 대해
e
=
w
G
s
{\displaystyle e=wG_{s}}
e 를 알 수 있다.
e
e
=
w
e
G
s
=
0.198
×
2.73
=
0.541
{\displaystyle e_{e}=w_{e}G_{s}=0.198\times 2.73=0.541}
e
e
=
e
0
−
Δ
e
,
e
0
=
e
e
+
Δ
e
=
0.541
+
Δ
e
{\displaystyle e_{e}=e_{0}-\Delta e,\quad e_{0}=e_{e}+\Delta e=0.541+\Delta e}
Δ
e
1
+
e
0
=
Δ
H
e
19
m
m
=
5
−
1.48
m
m
19
m
m
{\displaystyle {\frac {\Delta e}{1+e_{0}}}={\frac {\Delta H_{e}}{19mm}}={\frac {5-1.48mm}{19mm}}}
Δ
e
1.541
+
Δ
e
=
5
−
1.48
19
{\displaystyle {\frac {\Delta e}{1.541+\Delta e}}={\frac {5-1.48}{19}}}
Δe = 0.35 e0 = 0.541 + 0.35 = 0.891
e
0
=
H
v
H
s
=
H
−
H
s
H
s
=
19
−
H
s
H
s
=
0.891
{\displaystyle e_{0}={\frac {H_{v}}{H_{s}}}={\frac {H-H_{s}}{H_{s}}}={\frac {19-H_{s}}{H_{s}}}=0.891}
∴
H
s
=
10.048
m
m
{\displaystyle \therefore H_{s}=10.048mm}
Hs 를 구했다면 이제 각 단계별 e를 구해야 한다. e1 만 풀고 나머지는 반복 작업.
e
1
=
e
0
−
Δ
e
1
=
e
0
−
5
−
4.747
H
s
=
0.891
−
5
−
4.747
10.048
=
0.866
{\displaystyle {\begin{aligned}e_{1}&=e_{0}-\Delta e_{1}\\&=e_{0}-{\frac {5-4.747}{H_{s}}}\\&=0.891-{\frac {5-4.747}{10.048}}\\&=0.866\end{aligned}}}
반복작업은 엑셀로 계산해서 그래프를 그린다.
압력(kPa)
24시간 이후 다이얼게이지 읽음(mm)
Δe
e
0
5
0.891
54
4.747
0.02517914013
0.8658208599
107
4.493
0.02527866242
0.8405421975
214
4.108
0.0383160828
0.8022261146
429
3.449
0.06558519108
0.7366409236
858
2.608
0.08369824841
0.6529426752
1716
1.676
0.09275477707
0.5601878981
3432
0.737
0.09345143312
0.466736465
0
1.48
-0.07394506369
0.5406815287
완전 포화된 점토. 시료 초기 두께 20mm, 초기 함수비 24%, 비중 2.70, 시험결과 표는 다음과 같을 때, 체적변형계수 mv 계산
재하하중(kPa)
시료 두께(mm)
0
20
25
19.806
50
19.733
100
19.600
200
19.357
400
18.835
800
18.167
e
0
=
w
0
G
s
=
0.24
×
2.7
=
0.648
{\displaystyle e_{0}=w_{0}G_{s}=0.24\times 2.7=0.648}
재하하중(kPa)
시료 두께(mm)
ΔHf (mm)
0
20
0
25
19.806
0.194
50
19.733
0.267
100
19.600
0.400
200
19.357
0.643
400
18.835
1.165
800
18.167
1.833
Δ
e
e
1
+
e
0
=
Δ
H
e
H
0
{\displaystyle {\frac {\Delta e_{e}}{1+e_{0}}}={\frac {\Delta H_{e}}{H_{0}}}}
Δ
e
e
1
+
0.648
=
1.833
20
{\displaystyle {\frac {\Delta e_{e}}{1+0.648}}={\frac {1.833}{20}}}
Δ
e
e
=
0.151
=
Δ
H
e
H
s
=
1.833
H
s
{\displaystyle \Delta e_{e}=0.151={\frac {\Delta H_{e}}{H_{s}}}={\frac {1.833}{H_{s}}}}
∴
H
s
=
12.139
m
m
{\displaystyle \therefore H_{s}=12.139mm}
Δef 값을 계산한다.
Δ
e
f
=
Δ
H
f
H
s
{\displaystyle \Delta e_{f}={\frac {\Delta H_{f}}{H_{s}}}}
재하하중(kPa)
시료 두께(mm)
ΔHf (mm)
Δef
0
20
0
0
25
19.806
0.194
0.016
50
19.733
0.267
0.022
100
19.600
0.400
0.033
200
19.357
0.643
0.053
400
18.835
1.165
0.096
800
18.167
1.833
0.150
e 계산.
e
=
e
0
−
Δ
e
f
=
0.648
−
Δ
e
f
{\displaystyle e=e_{0}-\Delta e_{f}=0.648-\Delta e_{f}}
재하하중(kPa)
시료 두께(mm)
ΔHf (mm)
Δef
e
0
20
0
0
0.648
25
19.806
0.194
0.016
0.632
50
19.733
0.267
0.022
0.626
100
19.600
0.400
0.033
0.615
200
19.357
0.643
0.053
0.595
400
18.835
1.165
0.096
0.552
800
18.167
1.833
0.150
0.498
m
v
=
Δ
e
Δ
σ
1
+
e
{\displaystyle m_{v}={\frac {\frac {\Delta e}{\Delta \sigma }}{1+e}}}
하중 증분(kPa)
Δe
Δσ
1+e
mv (m2 /kN)
0 ~ 25
0.016
25
1.648
0.000388
25 ~ 50
0.006
25
1.632
0.000147
50 ~ 100
0.011
50
1.626
0.000135
100 ~ 200
0.020
100
1.615
0.000124
200 ~ 400
0.043
200
1.595
0.000135
400 ~ 800
0.054
400
1.552
0.000087
어떤 책[ 1] v 구할 때 분자의 1 + e에서 e를 쓰지 않고 하중 증분 단계의 평균 간극비 em 을 쓰기도 함.
q=49kPa, e0 =1.1, γsat =1.84t/m3 , H0 =10m인 포화점토층의 5m 깊이 1차압밀침하량 ΔH를 구하라. 단 P=9.2t/m2 일 때 e=1.04이며, 지하수위는 지표면에 있고 점토층 하단은 암반으로 되어있다.
풀이 1차 압밀침하량은
S
c
=
Δ
e
1
+
e
0
H
0
=
e
0
−
e
1
1
+
e
0
H
0
{\displaystyle S_{c}={\frac {\Delta e}{1+e_{0}}}H_{0}={\frac {e_{0}-e_{1}}{1+e_{0}}}H_{0}}
다른 값들은 주어져 있고, e1 만 구하면 된다.
P
0
=
(
γ
s
a
t
−
γ
w
)
H
0
2
=
(
1.84
−
1
)
×
5
=
4.2
t
/
m
2
{\displaystyle P_{0}=(\gamma _{sat}-\gamma _{w}){\frac {H_{0}}{2}}=(1.84-1)\times 5=4.2t/m^{2}}
Δ
P
=
q
=
49
k
P
a
=
5.0
t
/
m
2
{\displaystyle \Delta P=q=49kPa=5.0t/m^{2}}
P
0
+
Δ
P
=
9.2
t
/
m
2
{\displaystyle P_{0}+\Delta P=9.2t/m^{2}}
압밀 이후 하중
P
0
+
Δ
P
=
9.2
t
/
m
2
{\displaystyle P_{0}+\Delta P=9.2t/m^{2}}
1 =1.04이다.
∴
S
c
=
e
0
−
e
1
1
+
e
0
H
0
=
1.1
−
1.04
1
+
1.1
×
10
m
=
0.286
m
{\displaystyle \therefore S_{c}={\frac {e_{0}-e_{1}}{1+e_{0}}}H_{0}={\frac {1.1-1.04}{1+1.1}}\times 10m=0.286m}
오른쪽 그림에서 가장 아래 점토층의 1차 압밀침하량을 구하시오. 토층 상단에 작용하는 하중은 8.0t/m2 이다.
토층
종류
두께(m)
비고
1
순수 모래
1.5
γ
1
=
1.765
t
/
m
3
{\displaystyle \gamma _{1}=1.765t/m^{3}}
2
포화 모래
3.0
Gs =2.65
3
정규압밀 포화 점토
5.0
γ
s
a
t
3
=
1.865
t
/
m
3
{\displaystyle \gamma _{sat3}=1.865t/m^{3}}
0 =0.9 L =60%
풀이 정규압밀 점토에 대한 1차 압밀침하량은
S
c
=
C
c
1
+
e
0
H
log
p
¯
0
+
Δ
p
¯
p
¯
0
{\displaystyle S_{c}={\frac {C_{c}}{1+e_{0}}}H\log {\frac {{\bar {p}}_{0}+\Delta {\bar {p}}}{{\bar {p}}_{0}}}}
액성한계 wL 이 주어져있으므로 경험식을 통해 압축지수 Cc 를 구할 수 있다. 불교란 시료에 대해
C
c
=
0.009
(
w
L
−
10
)
=
0.009
(
60
−
10
)
=
0.45
{\displaystyle C_{c}=0.009(w_{L}-10)=0.009(60-10)=0.45}
H=z3 =5.0m
Δ
p
¯
=
8.0
t
/
m
2
{\displaystyle \Delta {\bar {p}}=8.0t/m^{2}}
점토층 중간 지점(
z
3
2
{\displaystyle {\frac {z_{3}}{2}}}
p
¯
0
{\displaystyle {\bar {p}}_{0}}
p
¯
0
=
γ
1
z
1
+
γ
s
u
b
2
z
2
+
γ
s
u
b
3
z
3
2
{\displaystyle {\bar {p}}_{0}=\gamma _{1}z_{1}+\gamma _{sub2}z_{2}+\gamma _{sub3}{\frac {z_{3}}{2}}}
γ
s
u
b
2
=
γ
s
a
t
2
−
γ
w
=
G
s
+
e
1
+
e
γ
w
−
γ
w
=
G
s
−
1
1
+
e
γ
w
=
2.65
−
1
1
+
0.7
×
1
=
0.971
t
/
m
3
{\displaystyle \gamma _{sub2}=\gamma _{sat2}-\gamma _{w}={\frac {G_{s}+e}{1+e}}\gamma _{w}-\gamma _{w}={\frac {G_{s}-1}{1+e}}\gamma _{w}={\frac {2.65-1}{1+0.7}}\times 1=0.971t/m^{3}}
γ
s
u
b
3
=
γ
s
a
t
3
−
γ
w
=
1.865
−
1
=
0.865
t
/
m
3
{\displaystyle \gamma _{sub3}=\gamma _{sat3}-\gamma _{w}=1.865-1=0.865t/m^{3}}
∴
p
¯
0
=
7.723
t
/
m
2
{\displaystyle \therefore {\bar {p}}_{0}=7.723t/m^{2}}
최종적으로 침하량을 구하면
S
c
=
0.3656
m
{\displaystyle S_{c}=0.3656m}
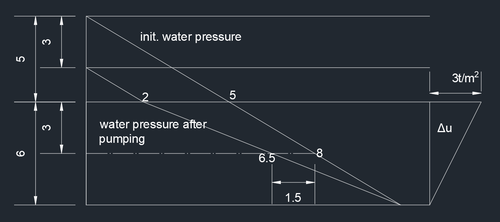
[ 편집 ] 양수작업 때문에 지하수위가 지표면에 위치하다가 3m 하강했을 때 압밀침하량 계산하기.
침하량 식
S
c
=
C
c
1
+
e
0
H
log
σ
0
′
+
Δ
σ
σ
0
′
{\displaystyle S_{c}={\frac {C_{c}}{1+e_{0}}}H\log {\frac {\sigma _{0}'+\Delta \sigma }{\sigma _{0}'}}}
이때 점토층 중앙에서 과잉간극수압 Δu = 1.5t/m2 이고,
σ
0
′
=
(
1.9
−
1
)
×
5
+
(
1.85
−
1
)
×
3
=
7.05
t
/
m
2
{\displaystyle {\sigma _{0}}'=(1.9-1)\times 5+(1.85-1)\times 3=7.05t/m^{2}}
이므로
S
c
=
0.43
1
+
0.9
×
6
m
×
log
7.05
+
1.5
7.05
=
0.114
m
{\displaystyle S_{c}={\frac {0.43}{1+0.9}}\times 6m\times \log {\frac {7.05+1.5}{7.05}}=0.114m}
단위중량 차로 인한 유효응력 감소분까지 고려한다면 점토층 중앙에서 지하수위 하강 후 전응력
σ
1
=
1.8
×
3
+
1.9
×
2
+
1.85
×
3
=
14.75
t
/
m
2
{\displaystyle \sigma _{1}=1.8\times 3+1.9\times 2+1.85\times 3=14.75t/m^{2}}
같은 지점에서 지하수위 하강 후 압밀완료 시 수압
u1 = 6.5t/m2 같은 지점에서 지하수위 하강 후 유효응력
σ
1
′
=
σ
1
−
u
1
=
8.25
t
/
m
2
{\displaystyle {\sigma _{1}}'=\sigma _{1}-u_{1}=8.25t/m^{2}}
∴
S
c
=
0.43
×
6
m
1
+
0.9
log
8.25
7.05
=
0.0927
m
{\displaystyle \therefore S_{c}={\frac {0.43\times 6m}{1+0.9}}\log {\frac {8.25}{7.05}}=0.0927m}
역시 로그 뒷부분만 변한다.
σ0 '은 동일. Δσ를 다르게 계산해야 함.
이땐
Δ
σ
=
γ
w
⋅
3
m
=
3
t
/
m
2
{\displaystyle \Delta \sigma =\gamma _{w}\cdot 3m=3t/m^{2}}
또는 이렇게 볼 수도 있다.
σ
1
′
=
σ
0
′
+
Δ
σ
=
γ
s
a
t
−
s
×
3
m
+
γ
s
u
b
−
s
×
2
m
+
γ
s
u
b
−
c
×
3
m
=
1.9
×
3
+
0.9
×
2
+
0.85
×
3
=
10.05
t
/
m
2
{\displaystyle {\begin{aligned}{\sigma _{1}}'&={\sigma _{0}}'+\Delta \sigma \\&={\color {red}\gamma _{sat-s}}\times 3m+\gamma _{sub-s}\times 2m+\gamma _{sub-c}\times 3m\\&=1.9\times 3+0.9\times 2+0.85\times 3\\&=10.05t/m^{2}\end{aligned}}}
이는
σ
0
′
+
Δ
σ
=
7.05
+
3
=
10.05
t
/
m
2
{\displaystyle {\sigma _{0}}'+\Delta \sigma =7.05+3=10.05t/m^{2}}
[ 2]
근데 이거 다른 책[ 3]
정규압밀점토 침하량이 Sc 라 할 때, 문제에서 60% 압밀 침하량이 얼마냐고 물어본다면 반드시 마지막에 0.6Sc 라고 답해야 한다.
무한등분포하중이 작용하는 점토층에 압밀이 진행중일 때의 연직유효응력을 묻는 경우. 전응력 = 유효응력 + 공극수압으로 푸는 게 아님. 압밀도와 과잉간극수압, 유효응력 사이의 관계를 이용해야 한다.
Δ
σ
′
=
Δ
σ
⋅
U
z
=
Δ
u
0
⋅
U
z
{\displaystyle \Delta \sigma '=\Delta \sigma \cdot U_{z}=\Delta u_{0}\cdot U_{z}}
σ
′
=
σ
0
′
+
Δ
σ
′
{\displaystyle \sigma '={\sigma _{0}}'+\Delta \sigma '}
그리고 깊이에 따라 연직유효응력 구해서 그래프 그리라는 문제에서 σ' 서로 다른 값 써야된다! z가 달라지면 σ'도 달라져!
1차 압밀침하 예제 2의 그림에 대해, 4년 후에 1차 압밀이 완료되며, 4년부터 10년까지 2차 압밀이 일어난다고 하자. 10년 후 전체 압밀침하량은? 단, 2차 압축지수 Ca =0.020이라고 한다.
풀이 정규압밀점토에 대해 2차 압밀량을 구한다.
S
s
=
C
a
1
+
e
p
H
log
t
2
t
1
{\displaystyle S_{s}={\frac {C_{a}}{1+e_{p}}}H\log {\frac {t_{2}}{t_{1}}}}
p 를 구한다. (얕보지 마라 이거 적어놓고 또 틀렸다)
e
0
−
e
p
=
Δ
e
=
C
c
[
log
(
p
¯
0
+
Δ
p
¯
)
−
log
p
¯
]
{\displaystyle e_{0}-e_{p}=\Delta e=C_{c}[\log({\bar {p}}_{0}+\Delta {\bar {p}})-\log {\bar {p}}]}
∴
e
p
=
e
0
−
C
c
[
log
(
p
¯
0
+
Δ
p
¯
)
−
log
p
¯
]
=
0.9
−
0.45
[
log
(
7.723
+
8.0
)
−
log
7.723
]
=
0.761
{\displaystyle \therefore e_{p}=e_{0}-C_{c}[\log({\bar {p}}_{0}+\Delta {\bar {p}})-\log {\bar {p}}]=0.9-0.45[\log(7.723+8.0)-\log 7.723]=0.761}
S
s
=
0.020
1
+
0.761
5.0
log
10
4
=
0.022597
m
{\displaystyle S_{s}={\frac {0.020}{1+0.761}}5.0\log {\frac {10}{4}}=0.022597m}
전체 압밀침하량은 1, 2차 압밀침하량을 더해서 구한다. 0.3656 + 0.022597 = 0.38820 m
log t법,
t
{\displaystyle {\sqrt {t}}}
t
{\displaystyle {\sqrt {t}}}
또 틀림
하부가 투수층인 8m 두께 점토층 원지반 위에 5m 높이로 성토하였다. 원지반 mv = 0.5 m2 /MN, cv = 10m2 /yr이다. 성토 완료 후 성토층 상부면 허용 침하량이 50mm이다. 그렇다면 성토 공사는 얼마나 빨리 완료할 수 있을까? 성토층 전체 단위중량은 2200kg/m3 이다. 성토하중은 모든 영역에서 즉시 작용한다고 가정한다.[ 4]
성토층 단위중량
γ
=
2200
k
g
/
m
3
×
9.8
m
/
s
2
=
21.56
k
N
/
m
3
{\displaystyle \gamma =2200kg/m^{3}\times 9.8m/s^{2}=21.56kN/m^{3}}
성토로 인한 응력 증가량
Δ
σ
=
21.56
k
N
/
m
3
×
5
m
=
107.8
k
N
/
m
2
{\displaystyle \Delta \sigma =21.56kN/m^{3}\times 5m=107.8kN/m^{2}}
침하량
S
c
=
Δ
σ
⋅
m
v
⋅
H
=
107.8
k
N
/
m
2
×
0.5
m
2
/
M
N
×
8
m
=
0.4312
m
{\displaystyle {\begin{aligned}S_{c}&=\Delta \sigma \cdot m_{v}\cdot H\\&=107.8kN/m^{2}\times 0.5m^{2}/MN\times 8m\\&=0.4312m\\\end{aligned}}}
이대로 압밀이 진행되면 성토층 상부 높이는 원지반에서 5 - 0.4312 = 4.5688m가 되어버린다. 이를 해결하기 위해 이렇게 생각해본다. z만큼 추가로 더 성토하고, z만큼이 침하된다면 결국 원지반으로부터 성토층 상부 높이가 5m가 될 것이다. 이 z를 구한다.
z를 더 성토하면 응력 증가량도 증가한다.
Δ
σ
=
(
5
+
z
)
×
21.56
k
N
/
m
2
{\displaystyle \Delta \sigma =(5+z)\times 21.56kN/m^{2}}
침하량
z
=
Δ
σ
⋅
m
v
⋅
H
=
(
5
+
z
)
×
21.56
k
N
/
m
2
×
0.5
m
2
/
M
N
×
8
m
{\displaystyle {\begin{aligned}z&=\Delta \sigma \cdot m_{v}\cdot H\\&=(5+z)\times 21.56kN/m^{2}\times 0.5m^{2}/MN\times 8m\\\end{aligned}}}
∴
z
=
0.472
m
{\displaystyle \therefore z=0.472m}
이제 성토공사 완료까지의 시간을 구할 것이다. 0.472m만큼이 다 침하되면 원하는 목표인 5m 성토가 완료된 것이다.(압밀도 = 100%) 그러나 허용침하량이 0이 아니라 0.050m이기 때문에 5 + 0.050 = 5.050m 높이까지만 압밀이 진행되었더라도 공사가 완료된 것으로 간주할 수 있다. 따라서 이때의 압밀도를 먼저 구한다.
U
a
v
g
=
0.472
−
0.050
0.472
=
0.894
{\displaystyle U_{avg}={\frac {0.472-0.050}{0.472}}=0.894}
즉 89.4% 압밀이 완료되었을 때 성토공사가 완료되었다고 볼 수 있다. 이제 89.4% 압밀에 걸리는 시간을 구한다.
T
v
=
1.781
−
0.933
log
(
100
−
U
a
v
g
(
%
)
)
=
0.824
{\displaystyle {\begin{aligned}T_{v}&=1.781-0.933\log(100-U_{avg}(\%))\\&=0.824\\\end{aligned}}}
t
=
T
v
⋅
H
d
r
2
c
v
=
0.824
×
4
2
m
2
10
m
2
/
y
r
=
1.32
y
e
a
r
s
{\displaystyle {\begin{aligned}t&={\frac {T_{v}\cdot {H_{dr}}^{2}}{c_{v}}}\\&={\frac {0.824\times 4^{2}m^{2}}{10m^{2}/yr}}\\&=1.32years\end{aligned}}}
Cc = 0.323, e0 = 0.855일 때
전체 침하량은 sand seam이 있을 때나 없을 때나 같다. [ 5]
그 과정은 아마 이럴 듯.
σ
0
1
′
=
17
×
2
+
(
19
−
9.8
)
×
6
+
(
20
−
9.8
)
×
4.5
2
=
112.15
{\displaystyle {\begin{aligned}{\sigma _{0_{1}}}'&=17\times 2+(19-9.8)\times 6+(20-9.8)\times {\frac {4.5}{2}}\\&=112.15\\\end{aligned}}}
S
c
1
=
0.323
1
+
0.855
×
4.5
log
112.5
+
60
112.5
=
0.146
m
{\displaystyle S_{c_{1}}={\frac {0.323}{1+0.855}}\times {\color {Red}4.5}\log {\frac {112.5+60}{112.5}}=0.146m}
σ
0
2
′
=
17
×
2
+
(
19
−
9.8
)
×
6
+
(
20
−
9.8
)
(
4.5
+
1.5
2
)
=
142.75
{\displaystyle {\begin{aligned}{\sigma _{0_{2}}}'&=17\times 2+(19-9.8)\times 6+(20-9.8)\left(4.5+{\frac {1.5}{2}}\right)\\&=142.75\\\end{aligned}}}
S
c
2
=
0.323
1
+
0.855
×
1.5
log
142.5
+
60
142.5
=
0.0398
m
{\displaystyle S_{c_{2}}={\frac {0.323}{1+0.855}}\times {\color {Red}1.5}\log {\frac {142.5+60}{142.5}}=0.0398m}
S
c
1
+
S
c
2
=
0.186
m
{\displaystyle S_{c_{1}}+S_{c_{2}}=0.186m}
그러나 3년 후 침하량은 달라진다.
풀이 과정은 각 구간의 Tv1 , Tv2 를 구하고, (조건으로 Cv = 1.26m2 /yr)
T
v
=
1.781
−
0.933
log
(
100
−
U
a
v
g
)
{\displaystyle T_{v}=1.781-0.933\log(100-U_{avg})}
avg1 , Uavg2 를 구한 뒤,
U
a
v
g
=
4.5
m
×
U
a
v
g
1
+
1.5
m
×
U
a
v
g
2
6
m
{\displaystyle U_{avg}={\frac {4.5m\times U_{avg_{1}}+1.5m\times U_{avg_{2}}}{6m}}}
avg 를 구한 뒤에 총침하량에 곱해서 3년 후 침하량을 구한다.
↑ 서상열, 김학삼 <<토질역학>> 272쪽
↑ 장연수, <<토질역학>>, 234쪽
↑ 이인모 <<토질역학의 원리>>
↑ Graham Barnes, <<Eurocode에 근거한 토질역학 이론과 실습>>, 185쪽
↑ 이인모, <<토질역학의 원리>>, 343쪽



























































![{\displaystyle e_{0}-e_{p}=\Delta e=C_{c}[\log({\bar {p}}_{0}+\Delta {\bar {p}})-\log {\bar {p}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/867e3ea502712633b84eff8dfb0896b4ed955ad1)
![{\displaystyle \therefore e_{p}=e_{0}-C_{c}[\log({\bar {p}}_{0}+\Delta {\bar {p}})-\log {\bar {p}}]=0.9-0.45[\log(7.723+8.0)-\log 7.723]=0.761}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68b43179c27c45748ef9ba5483ebded8192658f0)

















