사용자:Gcd822/토목기사 오답노트/수리수문학/개수로

용어 설명

• 수심(水深, depth of flow) : 공기와 물이 접하는 자유수면에서 수로 바닥까지의 연직 거리.
• 수위(水位, stage) : 자유수면으로부터 임의의 지점까지의 연직 거리.

비에너지

18-1, 18-2, 18-3, 19-1

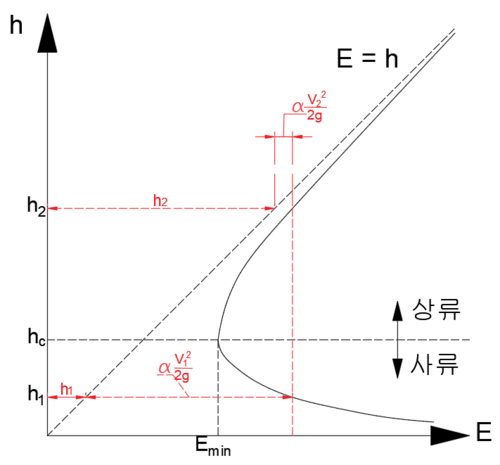
• ♣♣♣ 비에너지는 수로 바닥을 기준으로 한 단위무게의 물 에너지. 등류에선 일정.

15-1, 16-4, 19-2

$E=h+\alpha {\frac {V^{2}}{2g}}$

따라서 비에너지는 유량이 일정한 경우 수심만의 함수가 된다.

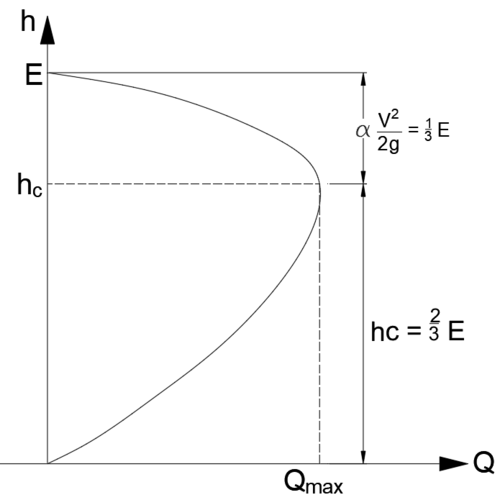
한계수심 : 비에너지가 최소일 때의 수심. 혹은 유량이 최대일 때의 수심 (정의 ♣♣14-2, 19-1, 19-3)

• 
• 
  ♣♣♣14-1, 15-1, 16-4, 19-3

95

개수로 단면이 오른쪽 그림처럼 w1에서 w2로 감소했다. 이때 수심 변화는 어떻게 될까?

---

풀이

• 상류인 경우: w2에서 유속 빨라짐. 수심 감소
• 사류인 경우: w2에서 유속 느려짐. 수심 증가

이유는 다음 그래프로 생각해보면 됨. 단위폭당 유량에 따른 수심변화와, 속도 수두가 어떻게 될 것인지....

수중 구조물이 있는 경우 수면 변화

상류의 흐름에 수중보를 설치하는 경우. 편의상 비에너지의 손실은 없다고 가정.

$E_{1}=h_{1}+{\frac {{V_{1}}^{2}}{2g}}$

$E_{2}=h_{2}+{\frac {{V_{2}}^{2}}{2g}}$

이것은 수로 바닥면이 z만큼 높아진 상태에서의 비에너지이다. 원래의 수로 바닥면과는 z의 높이만큼 비에너지 차이가 날 것이다. 비에너지의 손실은 없다고 하였으므로 1단면과 2단면의 비에너지가 같아야 한다. 이것을 식으로 나타낸다면

$E_{1}=E_{2}+z$

상류 흐름에 수중보를 설치하면 보가 있는 부분에서 수위는 감소. 같은 방법으로 사류일 때를 확인해보면 반대로 수위가 증가.

사각형 단면 한계수심

$h_{c}=\left({\frac {\alpha Q^{2}}{gb^{2}}}\right)^{\frac {1}{3}}$

---

97, 18-3

직사각형 수로에서 폭이 5m, 한계수심이 1m, 에너지 보정계수 α = 1.0이면 유량은?

---

$h_{c}=\left({\frac {\alpha Q^{2}}{gb^{2}}}\right)^{\frac {1}{3}}$

$Q=\left({\frac {{h_{c}}^{3}gb^{2}}{\alpha }}\right)^{\frac {1}{2}}=15.65m^{3}/s$

도수

= hydraulic jump. 흐름이 사류에서 상류로 변할 때 수면이 불연속적으로 뛰는 현상. 가지고 있는 에너지의 일부를 와류와 난류를 통해 소모한다.(15-1)

도수 전후 두 수심 : 공액수심

도수 후 수심 = 도수고

♣♣♣12-3, 14-3, 15-2, 16-1, 19-3

직사각형 단면에 대해

$h_{2}={\frac {h_{1}}{2}}\left(-1+{\sqrt {{\color {red}1}+{\color {red}8}{Fr_{1}}^{2}}}\right)$

• $Fr_{1}={\frac {V_{1}}{\sqrt {gh_{1}}}}$

도수 전후 비력이 일정함을 이용해 유도됨.(단위폭당 유량, 이차방정식 근의 공식, 프루드 수 등을 이용해 유도)

---

도수로 인한 에너지 손실

♣♣♣13-1, 14-2, 19-2, 19-3

$\Delta E={\frac {{\color {red}(}h_{2}-h_{1}{\color {red})^{3}}}{4h_{1}h_{2}}}$

비에너지 차이, 도수 전후 수심 유도 과정 중 나오는 식을 이용해 유도함.

---

참고 서적

• 김경호 (2010). 〈11. 개수로 정상흐름의 기초〉. 《수리학》. 한티미디어. 

오리피스

작은 오리피스

95, 19-2, 20-1+2

오리피스 수두 오차와 유량 오차의 관계

${\frac {dQ}{dH}}=CA{\sqrt {2g}}{\frac {1}{2}}H^{-{\frac {1}{2}}}$

${\frac {dQ}{Q}}={\frac {CA{\sqrt {2g}}}{Q\times 2{\sqrt {H}}}}dH$

${\frac {dQ}{Q}}={\frac {\cancel {CA{\sqrt {2g}}}}{{\cancel {CA}}{\sqrt {{\cancel {2g}}H}}\times 2{\sqrt {H}}}}dH$

${\frac {dQ}{Q}}={\frac {1}{2}}{\frac {dH}{H}}$

노즐

노즐

12, 18-2

유량

$Q=C{\frac {\pi d^{2}}{4}}{\sqrt {\frac {2gh}{1-C^{2}\left({\frac {d}{D}}\right)^{4}}}}$

위어

위어 월류 유량 공식의 일반형(02, 13-3)

$CL(h+h_{a})^{\frac {3}{2}}$

• C : 월류 계수
• L : 월류 폭

사각형 위어

유량

15-2

베르누이 방정식과 연속방정식을 결합한 뒤, 적분하여 유도

$Q={\frac {2}{3}}Cb{\sqrt {2g}}h^{\frac {3}{2}}$

프란시스 유량 산정 공식

01, 02, 18-3

$Q=1.84\left({\color {red}b}-{\frac {nh}{10}}\right)h^{\frac {3}{2}}$

• n : 양단 수축 2, 일단수축 1, 수축 없으면 0
• h : 월류수심

단수축 폭

18-1

$b_{0}=b-{\frac {nh}{10}}$

---

• 직사각형 수로에서 월류 수두 h와 유량 Q의 관계(99, 00, 12, 16-3, 19-1, 19-2)

${\frac {dQ}{Q}}={\frac {3}{2}}{\frac {dh}{h}}$

광정 위어

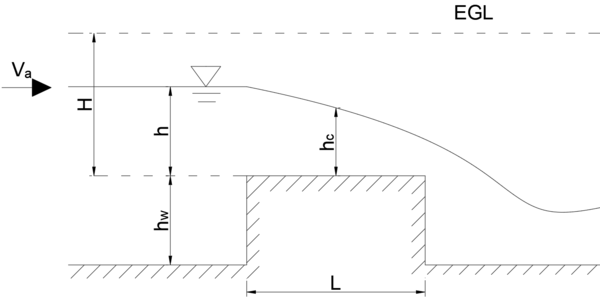
broad crest weir. 월류수심 h에 비해 위어 마루 폭 L이 큰 경우.(L > 0.7h)

(05, 13-1, 14-2, 20-1+2 ♣♣)

위어 상류의 한 지점과, 위어에서 한계수심 나타나는 한 지점사이에 베르누이 정리 사용하여 유량 공식 유도.

그림을 정확히 이해하고 유량 공식을 암기하기

${\begin{aligned}H=h+{\frac {{V_{a}}^{2}}{2g}}&=h_{c}+{\frac {{V_{c}}^{2}}{2g}}\\&={\frac {2}{3}}H+{\frac {{V_{c}}^{2}}{2g}}\\\end{aligned}}$

$V_{c}={\sqrt {\frac {2gH}{3}}}$

${\begin{aligned}Q=bh_{c}V_{c}&={\frac {2bH}{3}}{\sqrt {\frac {2gH}{3}}}\\&=1.7bH^{\frac {3}{2}}\\\end{aligned}}$

• H : 전수두(h + h_a)
• h : 월류수심
• $h_{a}=\alpha {\frac {{V_{a}}^{2}}{2g}}={\text{접 근 유 속 수 두 }}$
• $V_{a}$ : 접근유속

사다리꼴 광정 위어

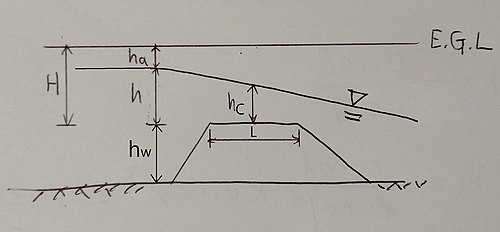
홈마 공식(실험에 의한 것)

$Q=Cb{\sqrt {2g}}h^{\frac {3}{2}}$

---

2. 96

(사다리꼴) 광정위어에서 유량이 30m³/s일 때 위어 상면 수심은? 위어 폭이 5m, m = 0.4

---

$Q=mb{\sqrt {2g}}h^{\frac {3}{2}}$

$h=\left({\frac {30}{0.4\times 5{\sqrt {2g}}}}\right)^{\frac {2}{3}}=2.26m$

삼각형 위어

삼각형 위어

♣♣♣97, 00, 01, 13-2, 14-3, 15-1

$Q={\frac {8}{15}}C\tan {\frac {\theta }{2}}{\sqrt {2g}}h^{\frac {5}{2}}$

• C : 유량계수

삼각형 수로에서 월류 수두 h와 유량 Q의 관계(93, 97, 98)

${\frac {dQ}{Q}}={\frac {5}{2}}{\frac {dh}{h}}$