상위 문서 : 포털:기술 공학/측량학
- 면적측량
- 직접법 : 현지에서 직접 거리, 각 측량하여 면적 계산
- 간접법 : 도상, 기하학 공식을 이용해 면적 계산
- 체적측량
- 단면법 : 단면간 토공량 계산 시
- 점고법 : 넓은 지역 택지공사 시
- 등고선법 : 건물 부지 정지 작업, 저수지 용량 산정 시

♣♣♣
사다리꼴 넓이 + 포물선 넓이 공식으로부터 유도된다.
![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+f(x_{n})+4\sum _{j=1}^{n/2}f(x_{\color {red}2j-1})+2\sum _{j=1}^{n/2-1}f(x_{\color {red}2j}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ca7681f119e79524345f79c7dbd605ccbf1b1db)
이 식에서  은 구간
은 구간 ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) 을 나눈 부분구간의 총 개수를 뜻하며 짝수여야 하고,
을 나눈 부분구간의 총 개수를 뜻하며 짝수여야 하고,  은 각 부분구간의 길이이다. 면적측량 시 n이 홀수라면 남는 부분은 사다리꼴의 넓이로 계산하여 더해준다. 이 공식을 정리하면 다음과 같이 쓸 수도 있다.
은 각 부분구간의 길이이다. 면적측량 시 n이 홀수라면 남는 부분은 사다리꼴의 넓이로 계산하여 더해준다. 이 공식을 정리하면 다음과 같이 쓸 수도 있다.
![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+...+4f(x_{n-1})+f(x_{n}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5676a54f555adca641facffd23308b8522c34035)

n이 3의 배수일 때 3개의 h씩 묶어 면적을 계산하여 다음 식으로 전체 면적을 구할 수도 있다. n이 3의 배수가 아니면, 2법칙을 적용하고 남는 구간은 심프슨 1법칙으로 계산해서 더한다.
![{\displaystyle {\frac {3}{8}}h[f(x_{0})+f(x_{n})+2\Sigma f(x_{\text{3의 배 수 }})+3\Sigma f(x_{\text{남 은 수 }})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6cf7ecd0d7326ab1323f646ae1bf8eab1aab832)
꼭짓점의 좌표가 차례로  인 삼각형을 생각하자. 각 꼭짓점의 좌푯값을
인 삼각형을 생각하자. 각 꼭짓점의 좌푯값을  에서부터 시작해 차례대로 적고, 그 아래에 다시
에서부터 시작해 차례대로 적고, 그 아래에 다시  를 적어 행렬의 꼴로 나타내면 다음과 같다.
를 적어 행렬의 꼴로 나타내면 다음과 같다.

우선 왼쪽 위에서 오른쪽 바로 한 칸 아래로 직선을 그으면 아래와 같이 된다.

이때 선으로 연결된 두 숫자를 곱해서 모두 더하면,  이다. 또, 오른쪽 위에서 왼쪽 바로 한 칸 아래로 직선을 그어 연결하면 아래와 같아진다.
이다. 또, 오른쪽 위에서 왼쪽 바로 한 칸 아래로 직선을 그어 연결하면 아래와 같아진다.
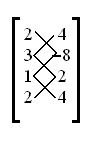
마찬가지로 이어진 두 수를 곱해 모두 더한 값은  이다. 여기서 두 값의 차의 절댓값에
이다. 여기서 두 값의 차의 절댓값에  을 곱하면
을 곱하면  이므로 이 삼각형의 넓이는 7이다.
이므로 이 삼각형의 넓이는 7이다.
양단면 면적차가 심할 때 산출된 토량의 대소관계 : 양단면 평균법(과대) > 각주공식(정확) > 중앙단면법(과소)
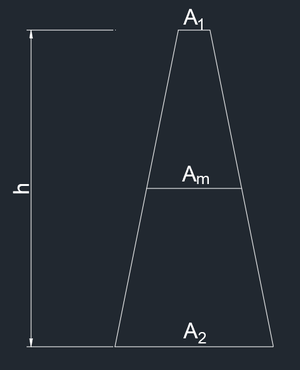
심프슨 1법칙 이용한 것. 가장 정확.



사각형 하나의 면적 A라 할 때


표준고 = 
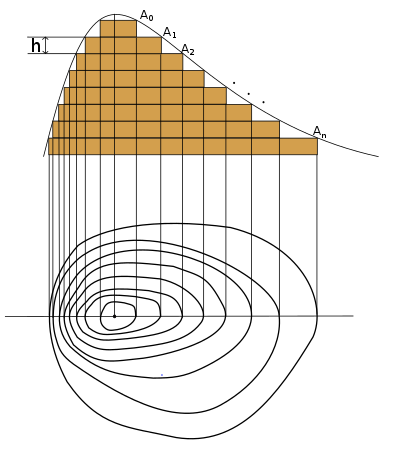
등고선을 이용해 체적을 구할 수 있다. 등고선법은 각주공식, 추대공식, 양단면 평균법으로 나눈다.
n은 짝수. 홀수일 경우는 짝수까지만 하고 남는 체적은 양단면 평균법으로 구해서 더함.








![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+f(x_{n})+4\sum _{j=1}^{n/2}f(x_{\color {red}2j-1})+2\sum _{j=1}^{n/2-1}f(x_{\color {red}2j}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ca7681f119e79524345f79c7dbd605ccbf1b1db)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {h}{3}}{\bigg [}f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+...+4f(x_{n-1})+f(x_{n}){\bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5676a54f555adca641facffd23308b8522c34035)
![{\displaystyle {\frac {3}{8}}h[f(x_{0})+f(x_{n})+2\Sigma f(x_{\text{3의 배 수 }})+3\Sigma f(x_{\text{남 은 수 }})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6cf7ecd0d7326ab1323f646ae1bf8eab1aab832)















