사용자:Gcd822/토목기사 오답노트/수리수문학/정수역학

압력 측정

16-4

h = 0.5m일 때 A, B 사이 압력차는? 수은 비중은 13.5

---

$P_{A}+0.5\times 9.8=P_{B}+0.5\times 13.5\times 9.8$

$P_{A}-P_{B}=0.5\times 12.5\times 9.8=61.25kN/m^{2}$

---

문제

P₁ = P₂일 때 원래 AA면에 수면이 위치하고 있다가 P₁이 증가하여 BB면으로 수면이 변했다. P₁ - P₂는?

---

수조 물 감소 = 액주계 물기둥 상승

${\cancel {\frac {\pi }{4}}}{d_{1}}^{2}\Delta h={\cancel {\frac {\pi }{4}}}{d_{2}}^{2}h$

$\Delta h={\frac {{d_{2}}^{2}}{{d_{1}}^{2}}}h$

BB면에서

$P_{1}=\gamma _{w}(\Delta h+h)+P_{2}$

${\begin{aligned}P_{1}-P_{2}&=\gamma _{w}(\Delta h+h)\\&=\gamma _{w}\left({\frac {{d_{2}}^{2}}{{d_{1}}^{2}}}h+h\right)\\&=\gamma _{w}h\left({\frac {{d_{2}}^{2}}{{d_{1}}^{2}}}+1\right)\end{aligned}}$

수중 물체에 작용하는 전수압

♣♣02

• 흐르지 않는 물에 잠긴 평판에 작용하는 전수압은 도심의 수압에 평판 면적을 곱해 구한다.
• 수심과 단면적이 같으면 전수압도 일정
• 전수압: 정수압에 면적 곱한 것[kg]
• 정수압: 정수 중 물의 압력 강도[kg/cm²]
• 수면에 평행한 평면에 작용하는 전수압은 평면의 도심에 작용

연직 평면에 작용하는 전수압

13-1

전면적 A에 작용하는 수압(h_c: 수면에서 도심까지의 깊이)

$F_{w}=\gamma _{w}{\color {red}h_{c}}A$

전수압의 작용점

$h_{p}=h_{c}+{\frac {I_{c}}{h_{c}A}}$

• $I_{c}$ : 도심에 대한 단면이차모멘트

---

10, 20-1+2

두 변의 길이가 3m인 직각이등변 삼각형의 한 변을 자유표면에 두면 자유표면으로부터 정수압의 작용점은?

풀이

정수압 작용점 $h_{p}=h_{c}+{\frac {\frac {bh^{3}}{36}}{h_{c}A}}=1.5m$

---

95

오른쪽 그림에서 단면에 작용하는 힘의 작용점은 AB로부터 수평으로 몇 m 떨어진 곳에 있는가?

풀이

ABCG, GDEF 단면으로 구분해서 각각의 전수압을 계산한다.

ABCG: $P_{1}=1t/m^{3}\times 1m\times 2m^{2}=2t$

GDEF: $P_{2}=1t/m^{3}\times 0.5m\times 1m^{2}=0.5t$

전단면: 2 + 0.5 = 2.5t

AB 면에서 각 단면 작용점까지 거리는

ABCG: ${\frac {AG}{2}}$

GDEF: $AG+{\frac {GF}{2}}$

이제 A에서 모멘트를 취한다.

$Px=P_{1}\times {\frac {AG}{2}}+P_{2}\times \left(AG+{\frac {GF}{2}}\right)$

$2.5t\times x=2t\times 0.5m+0.5t\times 1.5m$

x = 0.7m

---

16-2, 19-2 기출

수문에 작용하는 힘을 구하면?(kN 단위로)

---

정답

${\begin{aligned}P&={\frac {9.8\times 2+9.8\times 5}{2}}\times 3m\times {\color {red}2m}\\&=205.8kN\\\end{aligned}}$

차원을 생각해볼 것.

공식 $F_{w}=\gamma _{w}h_{c}A$에 대입해도 같은 결과가 나온다. 공식이 편하네.

---

오답(내가 자주 하는 착각)

$P={\frac {9.8\times 2+9.8\times 5}{2}}\times 3m\times 3m\times 2m\quad (X)$

경사진 평면에 작용하는 전수압

전수압

${\begin{aligned}F_{w}&=\gamma _{w}{\color {red}h_{c}}A\\&=\gamma _{w}y_{c}\sin \theta A\\\end{aligned}}$

O점에서 작용점 위치까지 경사깊이

$y_{p}=y_{c}+{\frac {I_{cx}}{y_{c}A}}$

• $I_{cx}$ : Ox축에 평행하면서 단면의 도심을 지나는 축에 대한 단면이차모멘트

수면에서 작용점 위치까지 연직깊이

$h_{p}=y_{p}\sin \theta$

---

참고 자료

• 임진근 외 (2015). 《토목기사 필기 - 수리수문학》. 성안당. 
• 김경호 (2010). 《수리학》. 한티미디어. 

곡면에 작용하는 전수압

♣98, 12-3, 14-1, 16-4

• 수평분력 P_H : 연직면에 투영한 면에 작용하는 전수압
• 수직분력 P_V : 곡면을 저면으로 하는 수면까지 수주 무게(투영면이 중복되는 부분은 빼줘야 함)
• 합력 $P={\sqrt {{P_{H}}^{2}+{P_{V}}^{2}}}$
• 작용점: w:바리뇽의 정리로 구함

---

96

길이방향으로 1m인 원통이 물을 막고 있다. 원통의 곡면에 작용하는 전수압을 구하시오.

풀이

수평수압은 연직방향으로 투영시킨 면에 작용하는 전수압과 같다.

$P_{H}=1t/m^{3}\times 2m^{2}\times 1m=2t$

수직수압은 곡면을 저면으로 하는 수주의 수면까지의 무게와 같다. 이때 중첩되는 부분은 계산에서 제외한다.

${\begin{aligned}P_{V}&=1t/m^{3}\times \left({\frac {\pi }{4}}\times 2^{2}m^{2}\times {\frac {1}{2}}\times 1m\right)\\&={\frac {\pi }{2}}t=1.57t\\\end{aligned}}$

전수압은 다음과 같이 구한다.

$P={\sqrt {{P_{H}}^{2}+{P_{V}}^{2}}}=2.54t$

---

11, 20-1+2

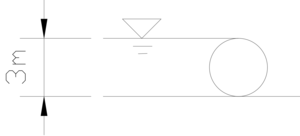
길이 8m인 드럼게이트에 작용하는 전수압이 수문에 작용하는 지점 수심을 구하시오.

---

풀이

수평, 연직 분력을 각각 먼저 계산하면 P_H = 36t, P_V = 9πt.

원의 중심 O에서 $x=1.5\cos \theta ,\quad y=1.5\sin \theta$

$\sum M_{O}=0$

P_H y = P_V x

$36\times 1.5\sin \theta =9\pi \times 1.5\cos \theta$

$\tan \theta ={\frac {9\pi \times 1.5}{36\times 1.5}}$

θ = 38.15도

수문의 작용점까지 수심

${\begin{aligned}h_{c}&=1.5m+y\\&=1.5+1.5\sin \theta \\&=2.43m\end{aligned}}$